A la une

Cet article est issu de la revue Dialogues économiques éditée par AMSE.
Pourquoi les coiffeurs se situent-ils toujours sur la même rue ? Quel est l’intérêt de mettre tous les restaurants et les cafés autour de la même place ? Comment expliquer ces heures d’errance sur la route, et puis, soudainement la présence de trois pompes à essence au même endroit ? Au-delà de la compétition sur les prix ou la qualité, il existe une concurrence pour l’espace. Les distances deviennent des ressources à se partager et les emplacements des objets de dispute.
Si plusieurs vendeurs de glace devaient se placer sur une plage, où se positionneraient-ils ? On peut supposer que chaque vendeur attire les consommateurs qui sont plus proches de lui que de ses concurrents. Mais leur choix s’établit en situation d’incertitude : ils ne savent pas où vont se placer les autres vendeurs. Comment résoudre cette énigme ? En économie, la théorie des jeux permet de modéliser ces situations où chaque agent ne connait pas à l’avance le choix des autres.
Stabilité dans l’anarchie
En utilisant cette théorie, les auteurs se sont penchés sur la compétition spatiale entre vendeurs. Ils souhaitent savoir s’il existe une solution dans laquelle la compétition pour les places pourrait se stabiliser durablement. Ils modélisent pour cela un réseau, à l’image d’un plan d’une ville, où plusieurs vendeurs doivent choisir l’emplacement de leur magasin parmi les nombreuses rues. Les acheteurs se promènent de façon homogène sur toutes les rues, et les vendeurs sont en concurrence : plus ils ont de clients, plus leur profit s’accroît. De leur côté, les clients achètent chez le vendeur le plus proche. Dans leur modèle, les auteurs n’envisagent ni une compétition sur les prix, ni sur les qualités, mais simplement sur la position géographique. Ils imaginent que les prix et les produits sont imposés aux vendeurs, à l’image des franchises de grandes entreprises ou encore des pharmacies par exemple.
Existe-t-il une situation dans laquelle tous les vendeurs sont satisfaits et ne souhaitent plus déménager ? Cette situation d’équilibre (appelé équilibre de Nash dans la théorie des jeux) est stable dans la durée parce qu’aucun des vendeurs n’aurait intérêt à changer de place tout seul, compte tenu du choix des autres vendeurs.
On pourrait penser que sur ce plan de ville, la libre-concurrence fait régner l’instabilité au point qu’aucune situation ne perdure dans le temps : tous les vendeurs se battraient continuellement pour une meilleure place. Toutefois, le modèle des auteurs montre que si le nombre de vendeurs est suffisamment grand,1 il existe un équilibre. À ce point d’équilibre, il est alors possible de cartographier l’emplacement des vendeurs et on sait qu’il restera fixe.2 C’est ce que les auteurs font : ils caractérisent cet « équilibre de Nash ». On sait que cet équilibre est stable car aucun des vendeurs ne changera de position seul : il y perdrait au change !
« Le prix de l’anarchie »
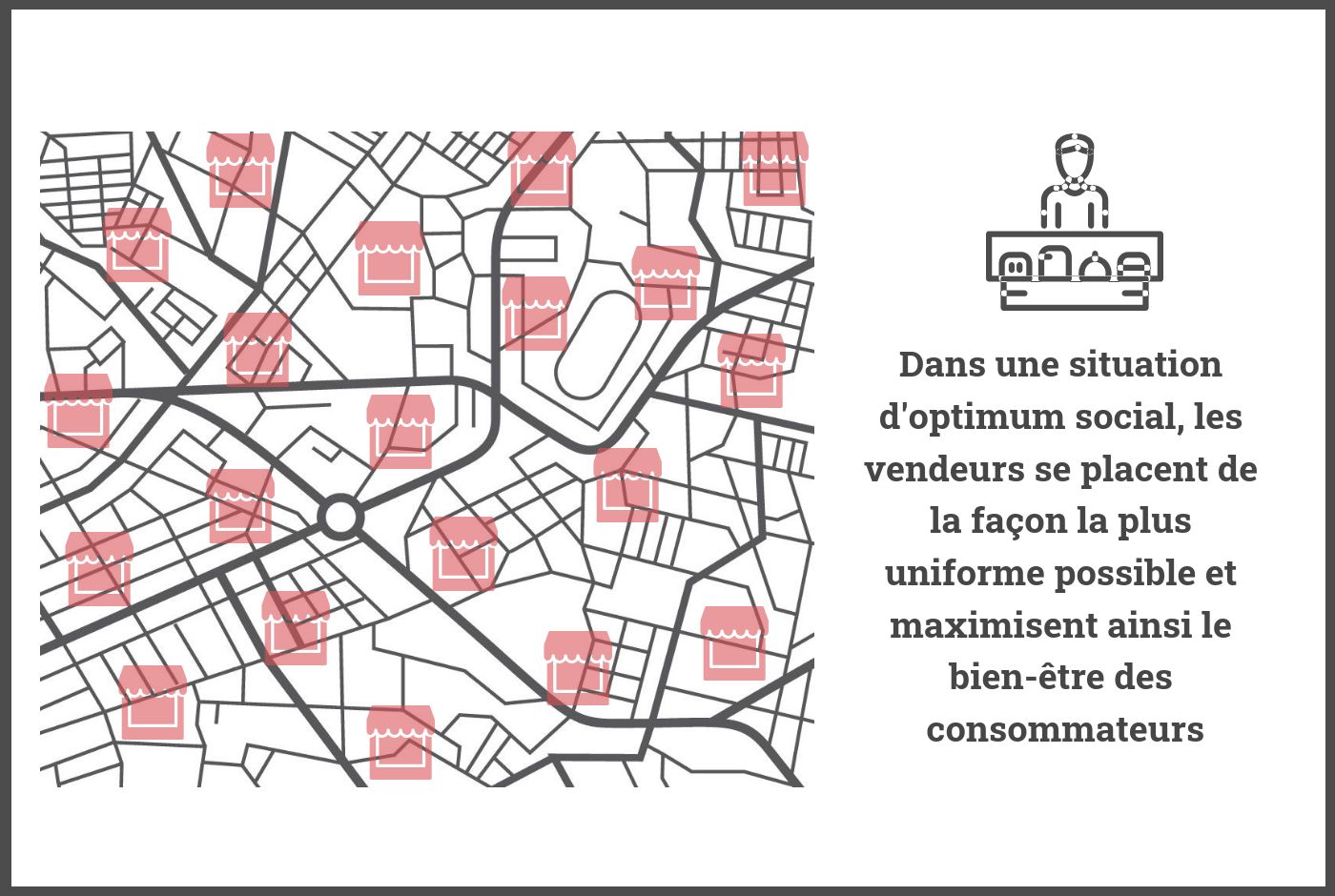
En plus du choix des vendeurs, il faut prendre en compte le bien être des consommateurs, ce que ne fait pas l’équilibre de Nash. Ici, il s’agit de la moyenne des distances réalisées par les clients pour acheter un bien. Dans une situation rêvée, la moyenne est la plus basse possible et permet aux acheteurs de se déplacer le moins possible. Cette situation, appelée l’optimum social, est idéale pour les consommateurs mais n’est pas un équilibre de Nash : elle est instable. Pour exister, cet optimum doit être protégé par une autorité publique. Par exemple, le ou la maire répartirait les vendeurs de façon la plus uniforme possible sur toutes les routes pour que les distances à parcourir par les clients soient les plus courtes possibles.

Pour savoir s’il est nécessaire de contraindre les vendeurs à respecter l’optimum social, le maire doit connaître le « prix de l’anarchie ». Cet outil compare ici la distance parcourue par les consommateurs dans une situation idéale et dans le pire des équilibres de Nash.
En effet, il n’existe pas une seule situation d’équilibre. Le choix opéré par les vendeurs en libre concurrence peut donner lieu à plusieurs scénarios différents. La répartition des vendeurs sur la carte peut alors s’avérer tout à fait différente.
Mais alors, qu’est-ce qui fait pencher la balance en faveur de l’un ou de l’autre des scénarios d’équilibre ? En économie, une discipline s’intéresse particulièrement à cette question : la théorie des jeux évolutive. Elle cherche à savoir comment la dynamique a été influencée pour converger vers un équilibre plutôt qu’un autre. Mais les auteurs ne cherchent pas à prédire un équilibre particulier. Ils imaginent que les vendeurs agissent en agents égoïstes, et que, par malchance, le pire des scénarios arrive : ils évaluent alors le « prix de l’anarchie ».
Ici, le coût est multiplié par deux : les acheteurs doivent se déplacer deux fois plus loin à l’équilibre que dans l’optimum. Cette conclusion pointe du doigt l’ampleur du décalage entre les pires scénarios de libre-concurrence et les situations idéales. Elle met en évidence comment la recherche égoïste du profit ne conduit pas nécessairement au bien commun. Alors que la collaboration ou la recherche du bien-être collectif pourrait réduire le coût social du consommateur, la libre-concurrence, elle, ne permet pas toujours d’atteindre un idéal social.
Référence :
Fournier G., Scarsini M., 2019, "Location Games on Networks: Existence and Efficiency of Equilibria," Mathematics of Operations Research, 44(1), 212-235
Notes :
1. Le nombre de vendeurs nécessaires à la formation d’un équilibre de Nash dépend de la structure de la ville (nombre et longueur des rues…)
2. Bien sûr, le modèle n’est pas toujours corroboré dans les situations réelles, puisqu’il ne prend pas en compte l’ensemble des paramètres de la réalité. De plus, le concept d’équilibre de Nash suppose que les vendeurs ne peuvent se déplacer en même temps ou s’entendre ensemble sur une solution à adopter. Toutefois, le modèle permet de dévoiler certains mécanismes économiques et de faire naître des questions utiles pour la société.



