A la une
Hormis une communauté de climatosceptiques, nul n’ignore désormais que le réchauffement climatique constitue une réalité tangible. On s’accorde aujourd’hui à penser que l’élévation de la température moyenne sur le globe terrestre est due à l’augmentation considérable de l’activité industrielle depuis le siècle dernier et de ses émissions massives de gaz dans l’atmosphère. Dès lors, la question se pose de savoir quelles conséquences cela aura sur la population vivante.
Indispensable modélisation
Celles-ci peuvent être d’ordres très divers. Ainsi, une augmentation de quelques degrés seulement est par exemple susceptible de provoquer la fonte des glaciers et élèverait le niveau des océans, pouvant causer des effets dévastateurs pour les populations vivant près des côtes. Des variations climatiques peuvent aussi occasionner des phénomènes météorologiques extrêmes – inondations, cyclones, ouragans ou même sécheresse –, constituant une menace dans des zones peuplées.
L’alimentation des espèces serait aussi transformée : l’ensemble des organismes vivants forme une chaîne alimentaire, structure complexe aux multiples maillons dans laquelle une espèce est mangée par une autre qui est à son tour mangée par une autre, et ainsi de suite. Si un maillon venait à disparaître, c’est toute la chaîne qui se retrouverait rompue. Ainsi, l’extinction du plancton dans les océans aurait un effet dramatique sur la pérennité des populations de poissons et sur le mode d’alimentation de l’Homme, dernier maillon de la chaîne.
Dans ce contexte, il apparaît essentiel de comprendre comment l’élévation – même minime – de la température moyenne peut avoir une influence sur un écosystème global comprenant l’Homme et les espèces animales et végétales qui l’entourent. Bien évidemment, cet écosystème est d’une complexité telle qu’il est hors de propos d’espérer décrire précisément son évolution et en tirer des enseignements sur l’effet de perturbations sur cet équilibre. Il est donc nécessaire de réviser ses ambitions à la baisse et de se limiter à des modèles beaucoup plus simples, mais dans lesquels une analyse deviendrait possible.
Partir du modèle le plus simple…
Il existe une grande variété de modèles écologiques faisant intervenir plusieurs espèces vivantes en compétition dans un cadre très simplifié, dans lequel chaque population correspond à une donnée qui varie dans le temps et dont on cherche à prédire l’évolution. En particulier, il convient de savoir comment les populations étudiées peuvent se comporter sur des temps longs : dans certains cas, on espère une stabilisation vers des valeurs d’équilibre ou des fluctuations périodiques autour de cet équilibre. Dans d’autres cas, il peut survenir une extinction d’une ou de toutes les espèces.
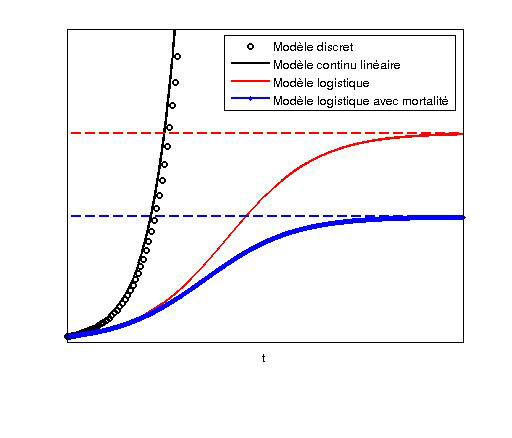
Comment construit-on un modèle ? Prenons pour commencer le cas – simple – de l’évolution d’une population unique. On veut décrire son effectif mesuré à des instants tn (l’indice n valant 0, 1, 2, 3 etc.) La fréquence des mesures va dépendre de l’ordre de grandeur de la variation du nombre d’individus : on ne mesure pas une population d’arbres aussi souvent qu’une population de bactéries. Ces temps sont donc séparés par des intervalles (que l’on notera Δt) qui peuvent être des secondes, des jours ou même des années selon le contexte. Cette population va être aussi caractérisée par un taux de croissance : plus la valeur de ce taux est grande, plus la population croîtra rapidement. La différence de population entre deux instants consécutifs tn et tn + 1 est alors proportionnelle à la population initiale, au taux de croissance et à l’intervalle de temps. C’est ce qu’on appelle un modèle discret.
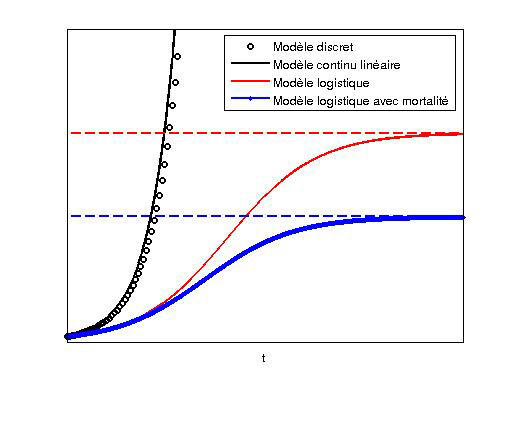
On peut aussi généraliser ce type de modèle au cas où la population est caractérisée par une grandeur non pas entière mais réelle , où le temps est « mesuré » en continu, et non plus à intervalles réguliers. L’idée est alors d’écrire une équation représentant l’évolution de la population en partant du modèle discret : on fait tendre l’intervalle de temps Δt vers 0. On aboutit alors à une équation différentielle bien connue et extrêmement fréquente en physique dont la solution peut être calculée explicitement. C’est le modèle continu le plus simple, appelé modèle linéaire.
Prendre en compte la taille maximale d’une population… et son taux de mortalité
Problème : dans le cadre de ce modèle linéaire, la taille de la population augmente indéfiniment, sans jamais se stabiliser à une valeur d’équilibre ! Autant dire que ce modèle n’est pas suffisamment réaliste pour représenter un phénomène de croissance réel. On lui préfère donc le modèle logistique, qui introduit un frein à la croissance de la population sous la forme d’une nouvelle constante baptisée facteur d’occupation maximale. On peut montrer que sur de longues périodes, la population va se rapprocher de ce « plafond », sans le dépasser. Notons que si on perturbe le taux de croissance, la valeur limite de la population n’en sera pas modifiée.
Pour parfaire ce modèle et prendre en compte la mortalité de l’espèce étudiée, on introduit un taux de mortalité. L’analyse de ce nouveau modèle logistique avec mortalité montre que si la mortalité est inférieure au temps de croissance, la population tend vers une valeur limite sur de longues échelles de temps. Dans le cas contraire, il y a extinction de l’espèce. Autre enseignement de ce modèle : si le taux de croissance est beaucoup plus grand que le taux de mortalité, une faible augmentation de ce dernier ne changera pas considérablement l’évolution générale de la population. Par contre, dans le cas où ces deux taux sont comparables, un changement radical peut alors survenir : l’on passe en effet d’une stabilisation d’une espèce… à son extinction ! Or le réchauffement climatique fait partie de ces facteurs extérieurs susceptibles d’augmenter le taux de mortalité…
Mêler les espèces étudiées
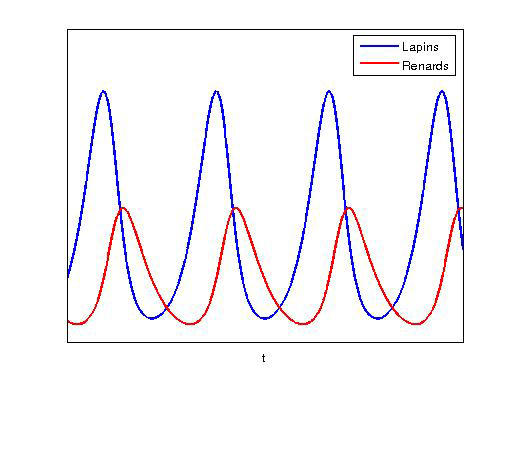
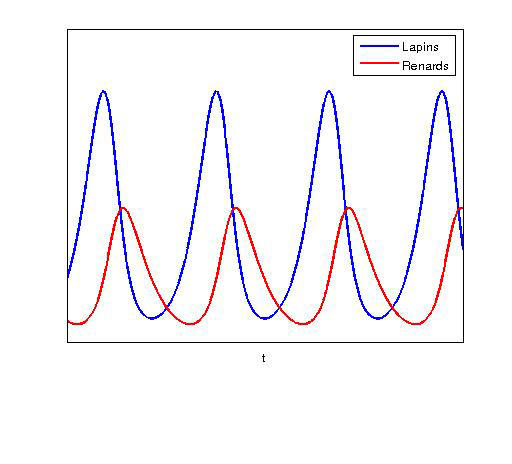
Lorsque l’on veut prendre en compte la croissance conjointe de plusieurs espèces, il faut considérer des modèles couplés. Il en existe plusieurs, bien connus des chercheurs en dynamique des populations. Un des plus célèbres est le modèle prédateur-proie connu sous le nom de modèle de Lotka-Volterra, dans lequel deux espèces (prédateurs et proies) sont en compétition. Cherchant là encore à décrire l’évolution de la population x de proies (par exemple des lapins) et y de prédateurs (par exemple des renards), on suppose qu’en l’absence de prédateurs, ces proies se développent exponentiellement vite en vertu du premier modèle décrit plus haut. En présence de prédateurs, il faut prendre en compte le taux de prédation qui causera une baisse de la croissance de la population de proies, proportionnelle au nombre de prédateurs. Il faut également considérer le taux de mortalité naturelle des prédateurs… ainsi que le fait que leur taux de croissance sera favorisé par la présence des proies.
On obtient ainsi un système qui ne possède pas de solution explicite, exprimable en fonction des populations initiales. Néanmoins, il aboutit à deux considérations intéressantes. La première : même si les populations initiales sont constamment très petites, c’est-à-dire proches de 0, il n’y aura pas, selon ce modèle, extinction des deux espèces en même temps. La seconde : il peut s’établir un équilibre cyclique entre les proies et les prédateurs, ces deux populations oscillant de manière périodique autour de leur valeur d’équilibre. Notons qu’une petite fluctuation de l’un des paramètres (comme l’augmentation du taux de prédation ou du taux de mortalité des prédateurs) ne changera pas le comportement sur des temps longs des deux populations étudiées.
Cas pratique dans une forêt des Ardennes
Une récente collaboration rémoise menée entre le Laboratoire de mathématiques de Reims1 et le Laboratoire Habiter de l’université de Reims Champagne-Ardenne a conduit à étudier la biodiversité d’un système socio-écologique correspondant à la population de la partie française du massif forestier des Ardennes2.
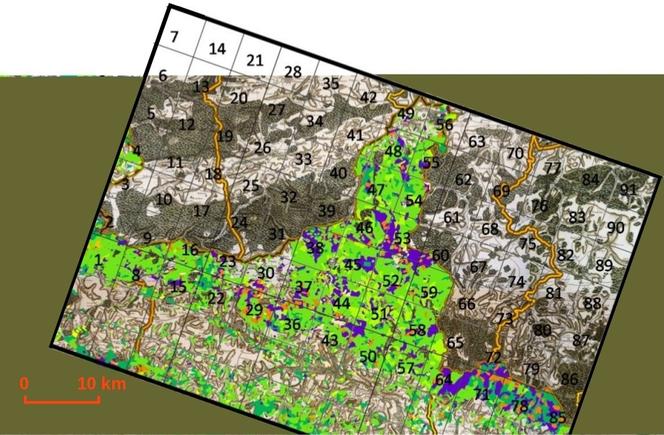
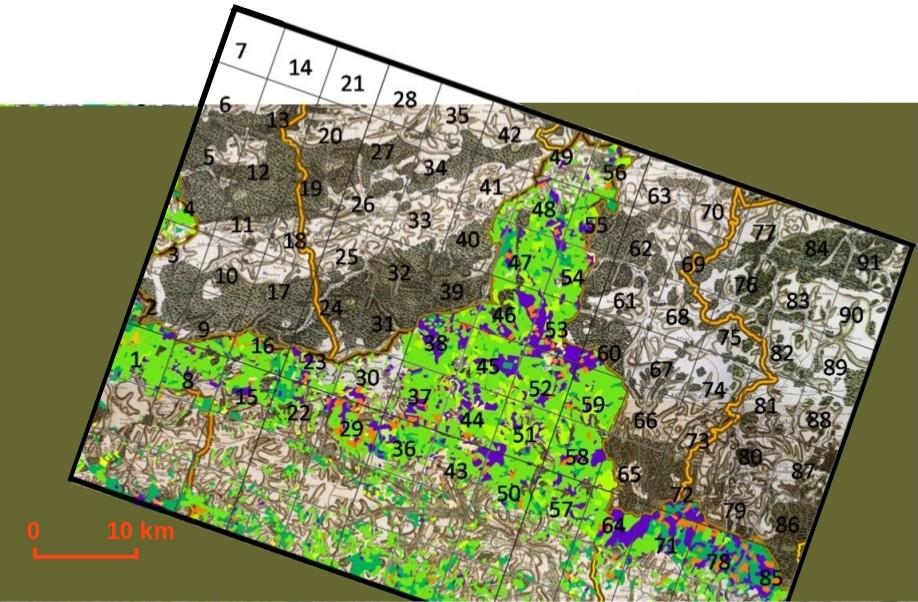
La stratégie a consisté à découper le massif considéré en plusieurs parcelles (comme indiqué sur la photo ci-contre), chacune d’entre elles étant peuplée par diverses espèces. On a alors choisi de séparer la population en deux espèces d’arbres (feuillus et résineux) selon des tranches d’âge différentes. Dans le cas le plus simple, on peut considérer trois tranches : les jeunes, les intermédiaires et les vieux, chacune étant caractérisée par des comportements différents. Ainsi, une population d’arbres jeunes aura un taux de croissance plus élevé que les autres tranches d’âge.
Ces populations sont toutes en interaction puisque la population des arbres jeunes va par exemple impacter la population future d’arbres intermédiaires et les vieux arbres vont à leur mort fournir de la matière pour le développement des jeunes arbres. On va donc utiliser pour chaque espèce un modèle de type logistique avec mortalité, dépendant de constantes de mortalité et de facteurs d’occupation relatifs à chaque espèce. Par ailleurs, on couple ces équations en introduisant dans le taux de croissance de chaque espèce une dépendance vis-à-vis de la population des autres espèces, à l’image de ce qui est fait dans le modèle proie-prédateurs précédemment évoqué (cf. figure 5). Chaque terme de croissance dépendant des populations d’arbres de tranches d’arbre voisines modélise la dépendance cyclique de la population d’arbres.
L’objectif de cette étude est de pouvoir effectuer des simulations pour divers scénarios dans le but de calculer un indice de biodiversité du milieu, grandeur mesurant en quelque sorte la qualité de l’écosystème, et d’analyser l’influence, sur cet indice, des variations climatiques qui vont faire fluctuer le taux de croissance ou encore le taux de mortalité. Cet indice de biodiversité dépend évidemment des caractéristiques de la parcelle de terrain considérée mais aussi de ses voisines pour tenir compte de la diversité écologique spatiale. Ainsi, une forêt homogène dans sa répartition écologique sera défavorisée au profit d’une forêt où les espèces ne sont pas présentes aux mêmes endroits. De façon sous-jacente, on cherche à voir dans quelle mesure ce massif ardennais peut s’adapter à un nouvel équilibre écologique avec des renouvellements périodiques des tranches d’âge, lorsqu’il est soumis à des perturbations telles que le réchauffement climatique. On parle de résilience du système écologique.
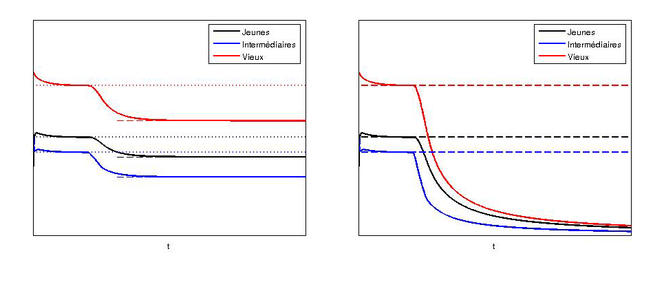
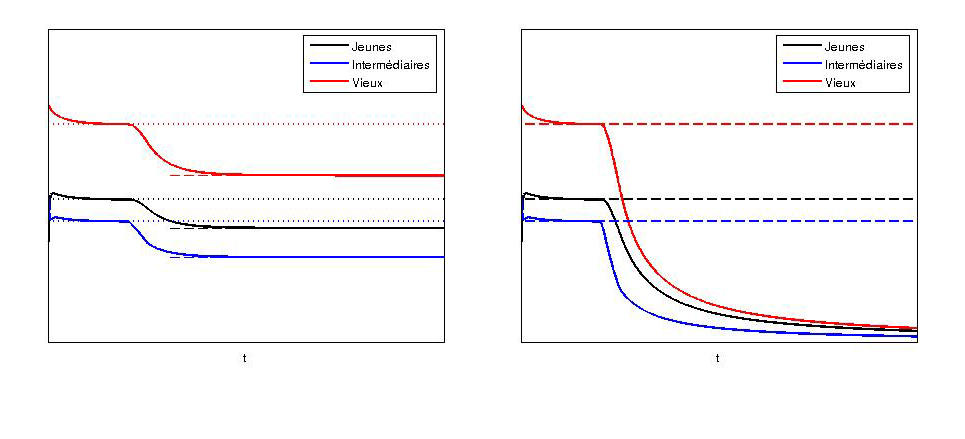
Une étude menée sur une seule parcelle a montré qu’une faible variation sur un seul taux de mortalité pouvait causer l’extinction de toutes les espèces dans des cas critiques (voir figure 5), contrairement au modèle prédateur-proie. Des situations plus réalistes nécessitant beaucoup plus de paramètres sont actuellement à l’étude et il est encore trop tôt pour conclure quoi que ce soit. Bien évidemment, il ne faut pas tirer de cette possibilité d’extinction dans une parcelle un constat trop alarmiste. En somme, un modèle mathématique jouet donnant une issue funeste à l’ensemble des espèces ne peut être vu comme l’arbre qui cache la forêt.
Les points de vue, les opinions et les analyses publiés dans cette rubrique n’engagent que leur auteur. Ils ne sauraient constituer une quelconque position du CNRS.
- 1. Ce laboratoire de l’université de Reims-Champagne-Ardenne fait partie de la fédération de recherche ARC-Mathématiques (CNRS/Université de Picardie Jules-Verne), dans laquelle on trouve également le LAMFA, (CNRS/Université de Picardie Jules-Verne) et le LMAC (université de technologie de Compiègne).
- 2. Ce travail a fait l’objet d’un financement PEPS MOMIS (Projet exploratoire premier soutien, Modélisation mathématique en interaction avec la société) en 2015 et 2016.