Vous êtes ici
Bretzels, bagels, donuts et... topologie
Les 4 et 5 octobre 2016, les médias étaient envahis par des bretzels, bagels et autres donuts. Le comité Nobel utilisait ces gourmandises pour tenter d’expliquer les travaux des trois physiciens lauréats, David J. Thouless, F. Duncan Haldane et J. Michael Kosterlitz. Les résultats étaient présentés comme très mathématiques... et donc un peu abscons ! Ces chercheurs étaient récompensés « pour les découvertes théoriques des transitions de phase topologique ». Pour le comité, « leurs découvertes ont permis des avancées dans la compréhension théorique des mystères de la matière et créé de nouvelles perspectives pour le développement de matériaux innovants ». Quel est le lien avec les bagels ? Quel rôle joue vraiment la topologie ?
« Transition de phase » ? Chauffons de l’eau à 100 °C…
N’importe quel matériau est soumis à des transitions de phase lorsque la température et la pression varient. Nous sommes par exemple habitués à ce que l’eau se transforme en glace à 0 °C et s’évapore à 100 °C. Les différentes phases (liquide, gazeuse, solide) d’un même objet, se caractérisent par une organisation très différente à l’échelle microscopique. Dans le solide, les atomes sont très organisés et sont rangés sur un réseau périodique quasi parfait. Ainsi, en connaissant la position de quelques atomes, on peut connaître la position de tous les autres avec une assez grande précision. On dit que les atomes sont corrélés à grande distance. À l’inverse, les atomes d’un gaz bougent incessamment et de façon imprévisible, si bien qu’il est impossible de savoir, à partir des positions de quelques-uns d’entre eux, ce que font les autres un peu plus loin. Lorsque la température est baissée progressivement et atteint des valeurs très précises (0 °C et 100 °C pour l’eau dans les conditions normales de pression), le système passe brutalement d’une phase à l’autre.

Alors que nous vivons dans un monde à trois dimensions, les théories de nos trois physiciens lauréats, Thouless, Haldane et Kosterlitz, concernent des mondes fictifs en une ou deux dimensions : il est possible d’étirer ou d’aplatir à l’extrême certains systèmes physiques pour qu’ils soient essentiellement linéaires ou planaires, et se comportent donc comme en dimension une ou deux. Mais qu’adviendrait-il de la transformation de l’eau en glace dans un monde à 1 ou 2 dimensions ? Léon Van Hove a apporté une réponse dans un théorème de 1950, ensuite généralisé par David Mermin et Herbert Wagner en 1966, puis finalement étendus à des systèmes plus généraux par de multiples auteurs. La conclusion de ces recherches est que, même à très faible température, les systèmes physiques à une ou deux dimensions ne peuvent jamais être corrélés à grande distance (théorème de Mermin-Wagner). Dit autrement, notre monde serait si différent en dimensions une ou deux que l’eau ne se transformerait jamais en glace.
Or, les chercheurs étaient très confus au début des années 1970, car des simulations numériques semblaient indiquer la présence d’une transition de phase pour divers systèmes bidimensionnels, ce qui contredisait ce théorème. En 1973, David J. Thouless et J. Michael Kosterlitz ont finalement compris ce qui se passait en deux dimensions, et c’est ce qui leur a valu le prix Nobel de cette année. Vadim Berezinskii, un physicien soviétique, avait fait des découvertes similaires mais moins abouties en 1970, ce qui fait qu’on parle souvent de transition BKT pour « Berezinskii – Kosterlitz – Thouless ». Malheureusement, Berezinskii est décédé en 1980 et n’a donc pu être récompensé cette année. Quant à F. Duncan Haldane, il a étudié des systèmes unidimensionnels et développé plus avant les propriétés topologiques des matériaux en petite dimension.

Donuts, bagels et bretzels, des exemples utiles
En quoi consiste cette « transition BKT » ? Kosterlitz et Thouless ont proposé que, dans un fluide en deux dimensions, des petits tourbillons pussent apparaître. Chaque tourbillon a un centre, et le fluide tourne autour de ce centre dans le sens des aiguilles d’une montre ou dans le sens inverse. Si on suit une particule du fluide au voisinage du tourbillon, elle se déplace essentiellement sur un chemin qui est enroulé autour du centre. C’est dans l’étude de ces chemins que l’on trouve les liens avec certaines notions mathématiques en topologie… et que les bretzels, les donuts et les bagels sont bien utiles pour comprendre la situation.
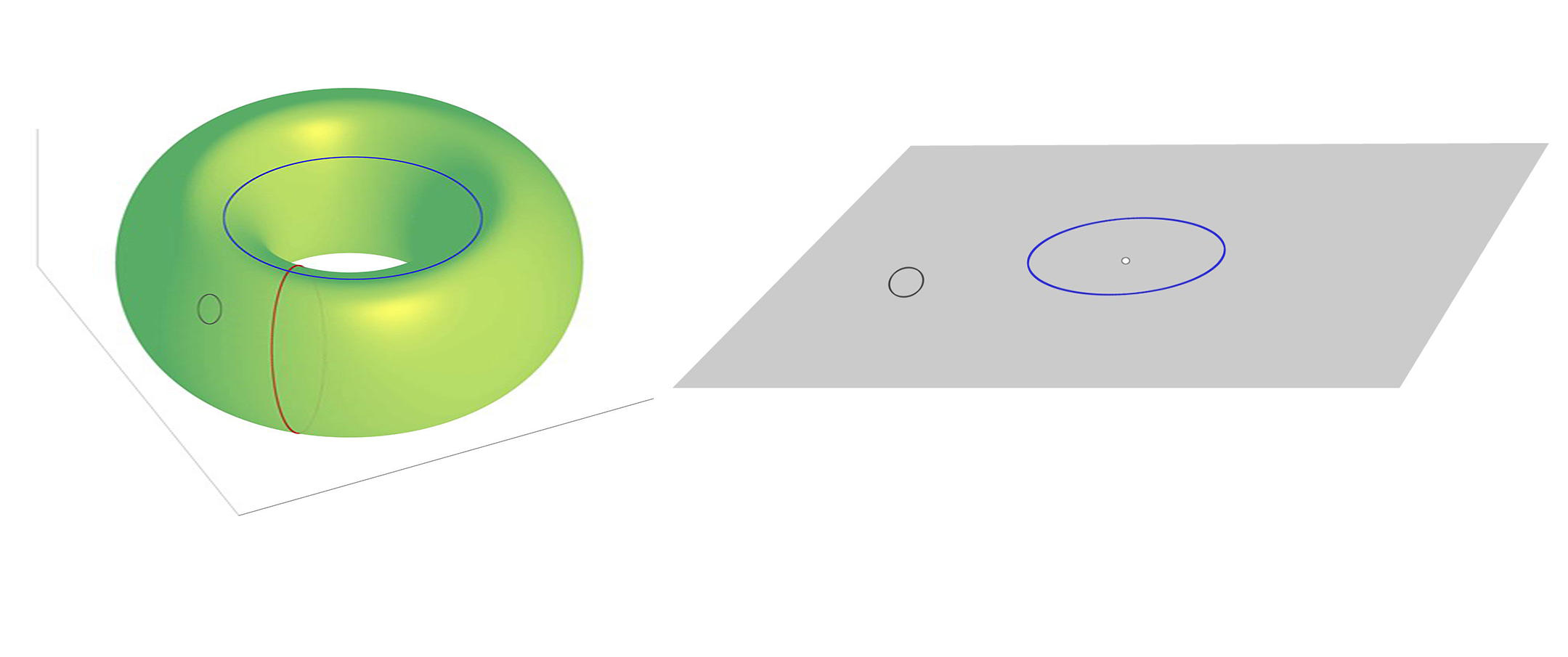
La théorie mathématique qui nous concerne ici est celle qui consiste à étudier la façon dont on peut déformer, contracter et déplacer des lacets sur des surfaces. Plaçons par exemple un élastique sur une sphère. On peut progressivement déformer cet élastique sans le décoller de la sphère et le contracter en un seul point choisi n’importe où sur celle-ci. Prenons maintenant un tore, une sorte de chambre à air qui ressemble à un bagel ou un donut. Du fait qu’il possède un trou, il y a diverses façons non identiques d’y placer un élastique. Un petit élastique posé sur le tore peut être déformé comme sur la sphère, mais un élastique qui est enroulé autour du tore ne peut jamais être contracté en un seul point. En fait, un tel élastique peut être enroulé autour de la chambre à air comme une bague autour d’un doigt, ou alors être posé sur le tore tout en faisant le tour de l’anneau (voir la figure ci-dessous). Ces deux nouvelles situations ne sont pas équivalentes : il est impossible de passer de l’une à l’autre en déformant l’élastique. Bien sûr, la classification de toutes les positions possibles des élastiques est encore plus complexe pour un bretzel qui a plusieurs trous.
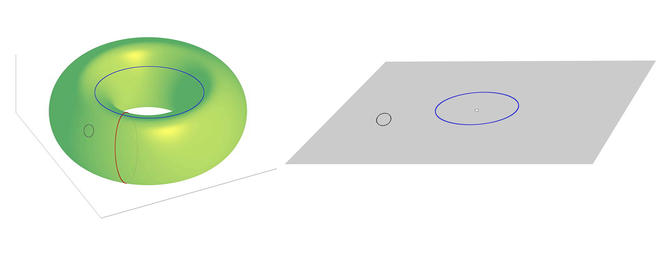
Les tourbillons étudiés par les physiciens sont en fait un peu plus simples que les donuts, les bagels et les bretzels. Prenons en effet un plan dans lequel on fait un trou (aussi petit que l’on veut). Un élastique placé loin du trou peut être déplacé et contracté en un point arbitraire du plan, mais un élastique enroulé autour du trou ne peut être contracté qu’en ce point et aucun autre. Par contre, si l’on se donne la liberté d’utiliser la troisième dimension, c’est-à-dire de sortir l’élastique du plan, ce phénomène disparaît complètement et toutes les manières de placer l’élastique redeviennent identiques. Faire un trou dans un plan est donc très différent de faire un trou dans l’espace à trois dimensions, du point de vue de la topologie. C’est l’une des raisons mathématiques pour lesquelles les systèmes physiques se comportent de façon très différente en deux dimensions.
Si Kosterlitz et Thouless utilisent dès leur premier article en 1973 l’expression « transition de phase topologique », la topologie intervient finalement de manière assez indirecte dans leurs travaux. Le trou mentionné précédemment correspond au centre du tourbillon et les élastiques aux chemins pris par les particules du fluide autour de ce dernier. Mais les arguments des physiciens n’utilisent pas directement le formalisme de la topologie. En revanche, leurs travaux ont ouvert la voie à une nouvelle manière de penser, et on a ensuite imaginé de nouveaux modèles pour lesquels la topologie intervient de manière beaucoup plus fondamentale.
Tourbillons et transitions de phase
Revenons aux tourbillons de Kosterlitz et Thouless. En 1973, les chercheurs ont eu l’idée géniale qu’à faible température, ce sont eux qui expliquent les propriétés spéciales des fluides en deux dimensions. En première approximation, les tourbillons s’attirent et se repoussent selon une loi universelle, qui ne dépend pas du fluide considéré, et qui est exactement la même que celle décrivant des particules chargées évoluant dans un plan. Deux tourbillons qui tournent dans le même sens se repoussent comme le font deux particules de même charge. Deux tourbillons tournant dans des sens différents s’attirent et peuvent s’annihiler.
Pour comprendre le rôle des tourbillons, Kosterlitz et Thouless les ont donc simplement remplacés par des particules chargées positivement et négativement, formant ce que l’on appelle un gaz de Coulomb ou un plasma à deux composantes. Ils ont montré qu’une transition de phase très spéciale avait lieu pour ce système simplifié. A une certaine température que l’on peut calculer exactement, les particules chargées positivement commencent soudainement à s’apparier avec des particules chargées négativement, puis le nombre de paires augmente quand la température diminue. C’est un type de transition de phase nouveau car il n’est pas brutal comme pour l’eau placée dans le congélateur. Les changements sont progressifs et difficilement détectables. Les particules chargées ne s’organisent pas sur un réseau comme pour un solide en trois dimensions, elles forment des couples indissociables mais libres, ce qui crée une forme d’ordre très faible à l’échelle microscopique.
Et maintenant…
La transition BKT constitue une source importante de problèmes mathématiques intéressants et difficiles. Dans un célèbre article de 1981, Jürg Fröhlich et Thomas Spencer ont réussi à démontrer l’existence d’une telle transition pour le gaz de Coulomb et d’autres systèmes du même type, confirmant ainsi les prédictions de Kosterlitz et Thouless. Pour y arriver, les deux chercheurs ont dû inventer d’une nouvelle méthode mathématique appelée « analyse multi-échelle » qui a ensuite été utilisée dans de multiples situations, n’ayant parfois rien à voir avec les transitions de phase.
Malheureusement, à ce jour on ne sait toujours pas prouver que dans le gaz de Coulomb la transition a bien lieu à la température prédite par Kosterlitz et Thouless. On ne sait pas non plus décrire précisément le comportement d’un fluide quelconque dans lequel apparaissent les tourbillons. L’attribution du Nobel de physique devrait relancer l’intérêt des mathématiciens pour ces questions fondamentales.
Les points de vue, les opinions et les analyses publiés dans cette rubrique n’engagent que leur auteur. Ils ne sauraient constituer une quelconque position du CNRS.