A la une

Cet article est issu de la revue Dialogues économiques éditée par AMSE.
Elon Musk, le patron de Tesla et SpaceX, touche en une seconde 500 dollars, soit ce que la moitié de la planète touche en un mois. L’importante augmentation, depuis les années 1980, des inégalités dans le monde suscite toute l’attention des économistes. Comment les mesurer ? Prendre en compte les revenus, le patrimoine, la moyenne, la médiane, les écarts interdéciles ? A. Atkinson et T. Piketty se sont intéressés aux revenus les plus élevés, S. Jenkins à la dynamique des revenus des ménages au Royaume-Uni, A. Krueger à l’augmentation des inégalités aux États-Unis.
Il existe cependant une mesure qui fait consensus depuis des années pour mesurer les inégalités : l’indice de Gini. Mis au point par le statisticien italien Corrado Gini du début du XXe siècle, cet indice prend la forme d’une valeur comprise entre 0 et 1, le zéro représentant l’égalité parfaite et le 1 l’inégalité la plus forte. Cette mesure est aujourd’hui massivement utilisée dans le monde pour analyser les inégalités entre les pays et au cours du temps. D’après la Banque mondiale, en 2021, la Suède a un coefficient de 0,298, la France 0,315 et le Brésil 0,529. En Chine, il est passé de 0,437 en 2010 à 0,371 en 2020, montrant une baisse des inégalités.
Les économistes Frank A. Cowell et Emmanuel Flachaire montrent que l’indice de Gini peut avoir un comportement inattendu. En augmentant le revenu d’une personne plus riche que la moyenne du groupe étudié, l’indice de Gini diminue les inégalités au lieu de les augmenter. Les chercheurs s’interrogent sur cette anomalie et étudient le comportement d’autres mesures d’inégalités, dans leur article "Inequality Measurement and the Rich : Why Inequality Increased More Than We Thought", publié en 2024 dans la revue The Review of Income and Wealth.
Propriétés des indices
Par une approche axiomatique, ils étudient les propriétés de l’indice ainsi que celles de deux autres mesures : l’indice de Theil et la mesure de dispersion logarithmique (MLD), toutes deux élaborées par Henri Theil, professeur néerlandais en économétrie dans les années 1960. Elles varient de 0, l’égalité parfaite, à l’infini, qui représente l’inégalité la plus forte.
Les indices de Gini, Theil et MLD mesurent la distance entre la distribution observée des revenus et une situation d’égalité parfaite où tous les individus reçoivent le même revenu. La distance est définie différemment selon la mesure utilisée. L’indice de Gini est basé sur des écarts en valeur absolue, alors que les indices de Theil et MLD utilisent des différences en logarithmes. Par ailleurs, l’indice de Theil est plus sensible aux variations dans les hauts revenus que les deux autres indices.
Les trois indices sont insensibles à l’échelle, c’est-à-dire que si on multiplie le revenu de tout le monde par deux, comme dans le cas d’une inflation par exemple, l’inégalité reste inchangée. Ce principe d’invariance à l’échelle stipule que les comparaisons d’inégalité ne doivent pas être affectées par des changements proportionnels dans les revenus ou les richesses. Il est respecté en divisant les revenus par leur moyenne, ce qui permet de comparer l’inégalité de manière indépendante de l’échelle absolue des données.
 Immeuble dont les fenêtres et les balcons ont l’apparence d’une règle graduée. Photo Debangshu Das sur Unsplash
Immeuble dont les fenêtres et les balcons ont l’apparence d’une règle graduée. Photo Debangshu Das sur Unsplash
Tous trois respectent également le principe des transferts, dit de « Pigou-Dalton » : tout transfert de revenu d’une personne plus riche vers une autre personne plus pauvre ne doit pas augmenter les inégalités. Par exemple, si une des personnes les plus riches donne 1 000 € à une des personnes les plus pauvres, les autres revenus étant inchangés, l’inégalité ne doit pas augmenter.
L’indice MLD est le seul à respecter un troisième principe, appelé « monotonicité en distance » : l’enrichissement d’un individu plus riche que le niveau d’égalité parfaite ne doit pas diminuer les inégalités, voire les augmenter, tout comme pour l’appauvrissement d’un individu plus pauvre. Fait surprenant : ce n’est pas le cas des indices de Gini et Theil. Avec ces derniers, l’inégalité totale peut diminuer quand on rend les riches encore plus riches. L’exemple ci-dessous en est la parfaite illustration : dans la situation B, le 5e individu voit son revenu augmenter de 20 €. La situation est jugée moins inégalitaire par les indices de Gini et Theil, alors qu’elle est jugée plus inégalitaire par l’indice MLD, car elle correspond à une situation où un individu ayant un revenu supérieur à la moyenne s’enrichit.

Moyenne ou médiane ?
Plus généralement, Frank A. Cowell et Emmanuel Flachaire cherchent à savoir s’il existe d’autres indices qui permettent de respecter simultanément le principe d’invariance à l’échelle et le principe de monotonicité en distance. Ils montrent que les indices classiques définis avec les revenus divisés par leur médiane, plutôt qu’avec les revenus divisés par leur moyenne, permettent de respecter ces deux principes. Ce résultat a un impact statistique important, car la moyenne est sensible aux valeurs extrêmes, contrairement à la médiane.
Dans le monde, la moyenne des revenus mensuels est de 1 392 dollars selon l’Observatoire des inégalités en 2021. Celle-ci inclut d’immenses fortunes, ce qui produit une moyenne à la hausse. Actuellement, Elon Musk, le patron de Tesla et SpaceX, représente une valeur extrême : il a demandé à ses actionnaires pour la période de 2018 à 2022 une rémunération de 56 milliards de dollars, soit 1,16 milliard de dollars par mois — plus de 800 000 fois la moyenne mondiale. De l’autre côté du spectre, les 2,5 milliards d’adultes représentant la moitié la plus pauvre de la population mondiale perçoivent moins de 558 euros par mois. Et en moyenne, ces 50 % les plus pauvres gagnent seulement 233 euros par mois — soit six fois moins que la moyenne mondiale. Si le monde était parfaitement égalitaire, chaque adulte toucherait 1 400 euros par mois.
Les calculs réalisés avec la médiane sont plus stables. Mais les indices d’inégalités basés sur les revenus divisés par la médiane ne respectent pas toujours le principe de transfert de Pigou-Dalton. Finalement, les chercheurs montrent qu’une seule mesure respecte tous les principes souhaités — invariance à l’échelle, transfert de Pigou-Dalton et monotonicité en distance — et, cerise sur le gâteau, n’utilise pas de division par la moyenne ou la médiane : c’est l’indice MLD.
Les inégalités ont plus augmenté que ce qu’on pensait
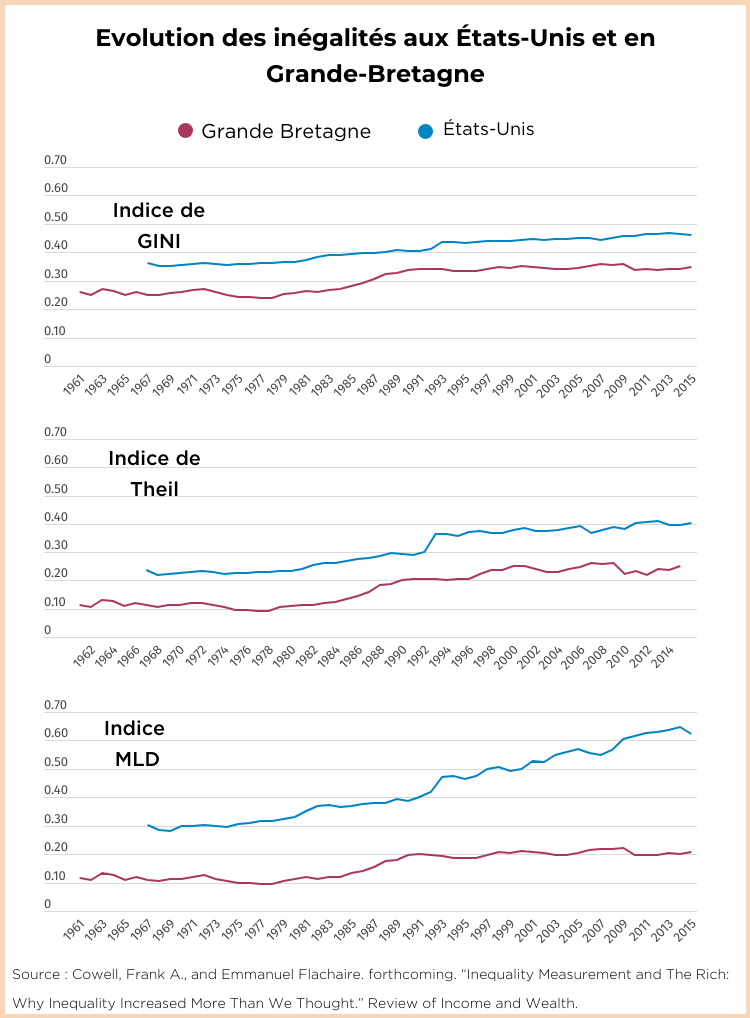
Dans l’analyse de l’évolution des inégalités aux États-Unis et au Royaume-Uni, des années 1960 à 2015, les indices de Gini et de Theil suggèrent une courbe assez similaire dans les deux pays. À l’inverse, l’indice MLD montre une augmentation des inégalités beaucoup plus marquée aux États-Unis qu’au Royaume-Uni, surtout à partir des années 1990. Ces résultats prouvent qu’une analyse basée uniquement sur l’indice de Gini ne permet pas de capturer aussi nettement la hausse des inégalités aux États-Unis que l’indice MLD.
Le choix des mesures d’inégalité est essentiel dans l’élaboration des politiques de réduction des inégalités. Dans les études de Thomas Piketty, c’est la proportion du revenu total détenue par une fraction des plus hauts revenus, comme le top 1 % ou top 10 %, qui est utilisée. C’est une mesure très intuitive et facile à comprendre pour le grand public. Selon la base de données du World Inequality Database, en 2022, les 1 % les plus riches captent 19,6 % des revenus mondiaux. Plus de la moitié des revenus revient aux 10 % les plus riches, et seulement 8 % des revenus à la moitié la plus pauvre. Mais ces mesures ne tiennent pas compte de la répartition des revenus au sein même des 1 % ou des 99 %. Autrement dit, une même valeur peut correspondre à des situations très différentes, où il y a beaucoup de pauvres ou très peu de pauvres dans la population.
Les indices de Gini, Theil ou MLD tiennent compte de la répartition des revenus dans l’ensemble de la population, ils permettent d’analyser la dynamique des inégalités et de faire des comparaisons entre pays, mais leurs valeurs ne sont pas aussi facilement interprétables, et ils peuvent conduire à des résultats sensiblement différents. En matière d’inégalités, s’il n’existe pas d’indice parfait, il est néanmoins important de bien connaître les propriétés des indices utilisés.
Référence :
Cowell F. A., Flachaire E., « Inequality Measurement and The Rich: Why Inequality Increased More Than We Thought. » Review of Income and Wealth, 71, no. 2: 254–77.



