Nos blogs

Le projet Frictional part du mouvement de l’archet sur les cordes pour mieux modéliser les systèmes dynamiques non-réguliers. Des avancées qui pourront servir aux virtuoses, mais aussi pour l’industrie et les sciences du climat.

Prédire le son précis que fera l’archet lorsqu’on le frotte sur les cordes d’un violon, c’est à la première écoute une histoire de musicien. Pourtant, c’est aussi un problème de physicien. « Les instruments à cordes frottées comme les violons ont un comportement complexe, ce qui explique qu’il soit si difficile d’en jouer », commence Soizic Terrien, physicienne du CNRS au Laboratoire d’acoustique de l’Université du Mans1 et responsable du projet Frictional, avec lequel elle s’attelle justement à l’analyse de ce comportement. « Leur son provient d’un mécanisme d’adhérence-glissement, ou stick and slip, c’est-à-dire une succession très rapide de phases d’adhérence de la corde puis de glissement, qui se passe plusieurs centaines de fois par seconde ». 

Un mécanisme avec des transitions brutales que les scientifiques savent modéliser et décrire grâce à des fonctions mathématiques, qui donnent des modèles dits non-réguliers, que l’on observe sous la forme de courbes « cassées ». « Aujourd’hui, il existe des modèles qui reproduisent dans les grandes lignes ces phénomènes, mais on ne sait pas encore dire précisément quel comportement est associé à quelle variation de paramètre ». Depuis 2023, une équipe formée au sein du Laboratoire d’acoustique de l’Université du Mans cherche donc à développer des modèles prédictifs fiables.

Frottements en tous genres

Pourtant, au laboratoire, pas de concert expérimental. « Une très grande partie de notre travail consiste en la recherche de méthodes de résolutions pour ces modèles mathématiques, qui diffèrent des systèmes qui varient de manière régulière », explique la chercheuse. Le développement des méthodes de résolution permet de créer une véritable cartographie des possibles avec les paramètres qui intéressent les scientifiques : où le musicien met son archet ? Selon quel angle joue-t-il ? L’archet appuie-t-il beaucoup ou peu sur la corde ? En fonction de cela, il est possible de trouver les frontières entre les différents régimes sonores en fonction des paramètres, donc dans quelle « zone » il n’y a pas de son, où il n’y en a qu’un seul possible et, « ce qui arrive le plus souvent, les zones dans lesquelles il y a plusieurs sons possibles. Dans ce cas, c’est au musicien de trouver la stratégie qui lui permettra d’accéder à l’un ou à l’autre ».

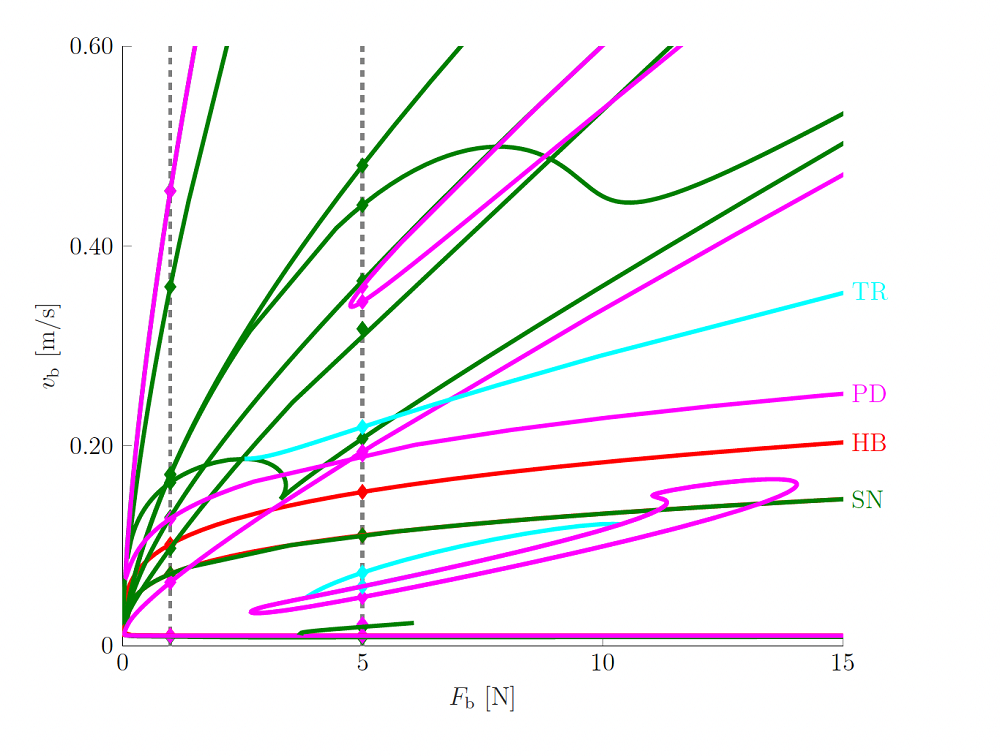
Cartographie des régimes sonores d’un modèle très simplifié de violon. Les différentes courbes correspondent à des « frontières » entre des comportements (donc des sons) différents et celles-ci sont représentées dans un espace des paramètres de contrôle du musicien, en l'occurrence la vitesse de l’archet et la force avec laquelle l’archet appui sur la corde. Comme sur une mappemonde, il faut imaginer que lorsque le musicien se « promène » dans cet espace, il peut observer un changement de régime sonore à chaque fois qu’une frontière (qu’on appelle ici des courbes de bifurcation) est traversée © Soizic Terrien, LAUM (CNRS/Le Mans Univ)

Ces recherches permettraient de savoir, par exemple, si un système produira du son – et lequel- avant de le construire. « Le frottement intervient de manière fortuite dans énormément de systèmes physiques, dès lors qu’il y a deux pièces qui entrent en contact. On peut donc intégrer ces modèles mathématiques dans de très nombreux autres champs de recherche et pour de très nombreuses applications, dans l’objectif notamment d’éviter des vibrations induites par le frottement, qui peuvent endommager les mécanismes. Il y a des applications en physique des instruments de musique et dans la lutherie, mais ce n’est finalement qu’un aspect parmi d’autres ! » L’amélioration des modèles mathématiques et des méthodes de résolution peut ainsi servir d’autres domaines : construction d’engins de forage, conception de systèmes de freins des voitures ou encore prévision des séismes.

Des équations plutôt que des violons

Une autre partie du projet a consisté à « désosser » un violon pour construire un système capable de l’imiter, pour capturer l’essentiel des mécanismes de production du son, mais avec moins de complexité. « Ce système minimal est composé d’une roue sur une petite masse en bois, encadrée par des réglets. La roue entraîne le morceau de bois, qui est ensuite rappelé à l’ordre par les réglets qui le retiennent. Cela reproduit le mécanisme d’oscillation d’une corde, à l’origine de la production du son du violon ». Une installation bien différente de l’instrument, mais qui permet aux scientifiques de s’affranchir de nombreux paramètres peu maitrisables, comme les modifications de tension des cordes du violon ou la géométrie de la caisse de l’instrument, qui peut varier avec la température et l’humidité ambiante. « L’idée, c’est d’aller chercher les ingrédients essentiels pour reproduire le mécanisme physique, et de rajouter ensuite, petit à petit, les éléments de complexité, pour arriver à une compréhension très fine de la production du son par ce type de frottement ». 

Photo légendée d’un banc expérimental (le « moins simplifié ») où une corde (sans le reste du violon) est frottée par un archet. Ici, l’archet est actionné par un bras robotisé dont la vitesse est contrôlée. La force d’appui archet/corde est également contrôlée. Ces deux paramètres sont normalement des paramètres de contrôle du musicien, qui évoluent en permanence en situation de jeu. Le fait ici de les contrôler (voire de les fixer le temps de faire une mesure) nous permet de caractériser objectivement leur influence sur le son produit, et d’accéder à des mesures répétables. © Soizic Terrien, LAUM (CNRS/Le Mans Univ)

Et effectivement, il reste beaucoup à découvrir, notamment en prenant en compte de nouveaux éléments que cette méthode a permis de mettre en avant comme étant déterminants. « Pendant longtemps, on a étudié la dynamique des systèmes en pensant que tout était constant dans le temps. Mais ce n’est pas du tout ce qu’il se passe dans la réalité : la pression que le musicien exerce sur l’archet dans notre système, la température moyenne dans un autre, ce sont des paramètres dont l’évolution dans le temps à une importance fondamentale, autant que la valeur des paramètres elle-même ». Dans les systèmes non-linéaires, la sensibilité est très importante et peut même donner une impression d’imprédictibilité, alors qu’il n’y a rien d’aléatoire, mais que de tout petits changements de paramètres peuvent mener à des comportements très différents. « Pour le son d’un violon, si par exemple on augmente la vitesse de l’archet, comme le font les musiciens au cours du jeu, on observe à un moment donné un changement brutal vers un tout autre son. Si l'on diminue ensuite cette vitesse pour revenir à sa valeur initiale, on ne retrouve pas les mêmes changements !  Ce qui nous semble être deux fois la même chose ne produit donc pas le même effet. C’est ce qui nous a mis sur la piste de l’importance du sens de variation du paramètre, ainsi que de la prise en compte de l’histoire du système ».

De la physique des instruments à celle du climat 

Alors quand on lui parle de l’aboutissement du projet, Soizic Terrien sourit : « Chaque fois qu’on trouve quelque chose, dix nouvelles questions arrivent ». Mais de premiers résultats sont déjà là, « notamment sur les méthodes qui permettent d’obtenir des cartographies de régimes sur les systèmes non-réguliers. Et comme elles ne sont pas spécifiques à notre sujet d’étude, elles peuvent servir à d’autres collègues qui étudient des choses qui se modélisent avec le même type d’équations… Comme le système climatique ! ». Alors que le système climatique se prête très mal aux expérimentations, l’avantage du système de friction minimal développé pour le projet Frictional est de pouvoir les permettre facilement, et en laboratoire.

« L’un des résultats majeurs de ce projet, qui est sûrement celui sur lequel nous allons continuer ensuite, c’est de démontrer que la vitesse de variation des paramètres dans le temps, qui n’était pas prise en compte auparavant et qui peut paraître insignifiante, peut en fait avoir un effet fondamental sur le résultat. En musique, cela revient à prendre en compte le jeu du musicien et ses gestes dans la production du son. » Un terrain d’exploration immense, qui commence par une démonstration sur le système minimal développé en laboratoire, mais qui pourrait ensuite aider, entre de nombreux autres domaines, les physiciens du climat à peaufiner leurs modèles « C’est une démonstration expérimentale d’un phénomène beaucoup plus général en dynamique non-linéaire. Pour les modélisations mathématiques du climat, cela peut mener à une meilleure compréhension des phénomènes de bascule. » En fin de compte, du violon au climat, il n’y a qu’un pas. 

Soizic Terrien devant son dispositif expérimental permettant d’imiter un violon, afin de capturer l’essentiel des mécanismes de production du son, mais avec moins de complexité © Ville du Mans Matthieu Picouleau

****************

Ces recherches ont été financées en tout ou partie par l’Agence Nationale de la Recherche (ANR) au titre du projet « Production du son par friction : analyse de bifurcation numérique et expérimentale pour les systèmes dynamiques non-réguliers – FRICTIONAL ». Cette communication est réalisée et financée dans le cadre de l’appel à projet Sciences Avec et Pour la Société - Culture Scientifique Technique et Industrielle pour les projets JCJC et PRC des appels à projets génériques 2022 (SAPS-CSTI-JCJC et PRC AAPG 2022).