Vous êtes ici
Entrez dans les matrices !
Tableaux Excel, modélisation climatique, simulation de la structure d’une aile d’avion, calcul dans un réseau de neurones, traitement des images… Derrière ces objets ou problèmes se cachent souvent des matrices. Tout droit issues de l’algèbre, elles sont avant tout des objets mathématiques sur lesquels on peut effectuer des opérations, comme on le fait avec des nombres. Parmi elles, la multiplication, une opération simple mais qui peut réclamer d’énormes ressources de calcul à un ordinateur lorsque la matrice devient grande. C’est pourquoi depuis les années 1960 des chercheurs s’attèlent à trouver des méthodes de multiplication optimisée afin d’accélérer ces calculs.
Les matrices peuvent être vues comme un tableau de valeurs. Elles permettent, entre autres, de décrire un système d’équations linéaires de manière compacte. La plupart des phénomènes physiques, chimiques ou biologiques peuvent ainsi être représentés sous forme de matrices. Les matrices sont aussi utilisées pour caractériser un objet, comme une image décrite par un tableau indiquant la valeur (couleur, position, etc.) de chacun de ses pixels, ou encore en machine learning (apprentissage automatique), où « l’essentiel du calcul dans un réseau de neurones est effectué sur des matrices représentant l’état de chacun des neurones », pointe Gabriel Peyré, chercheur au Département de mathématiques et applications de l’École normale supérieure1.
Des tableaux aux matrices
Les ancêtres des matrices ont vu le jour en Chine, au Ier siècle avant ou après notre ère. « Dans l’ouvrage anonyme Les neufs chapitres sur les procédures mathématiques, on trouve quelque chose qui ressemble à une matrice. Car la procédure pour résoudre un système linéaire commence par décrire une mise en tableau des données », expose Karine Chemla, chercheuse en histoire des mathématiques au laboratoire Science, Philosophie, Histoire (Sphere)2. L’intérêt de cette mise en page est comparable à notre numération positionnelle qui permet d’additionner facilement en superposant les unités, les dizaines, les centaines, etc. « L’idée ici est que l’algorithme de résolution du problème s’appuie sur la disposition des données en tableau », souligne-t-elle.
Pour autant, ces tableaux ne peuvent pas encore être considérés comme des matrices car ils ne peuvent être utilisés pour faire des opérations. « Ce saut va se faire au milieu du XIXe siècle, avec les travaux d’Arthur Cayley », indique Karine Chemla. Ce mathématicien britannique pose les premières opérations élémentaires sur ces objets : addition, inversion ou multiplication. Opérer sur les matrices lui permet de résoudre des problèmes de géométrie. En effet, la transformation géométrique d’un objet – sa rotation par exemple – peut être écrite grâce à une matrice. Et la succession de plusieurs transformations n’est rien d’autre que la multiplication de matrices représentant chacune une transformation géométrique que subirait ce même objet. Une technique très utilisée dans le graphisme 3D.
Dans un monde toujours plus numérique, la multiplication matricielle est devenue une opération centrale, et pas seulement dans le champ des mathématiques. « Presque tous les algorithmes utilisent la multiplication matricielle pour faire de la résolution numérique », rappelle François Le Gall, chercheur à la Graduate School of Mathematics de l’université de Nagoya (Japon).
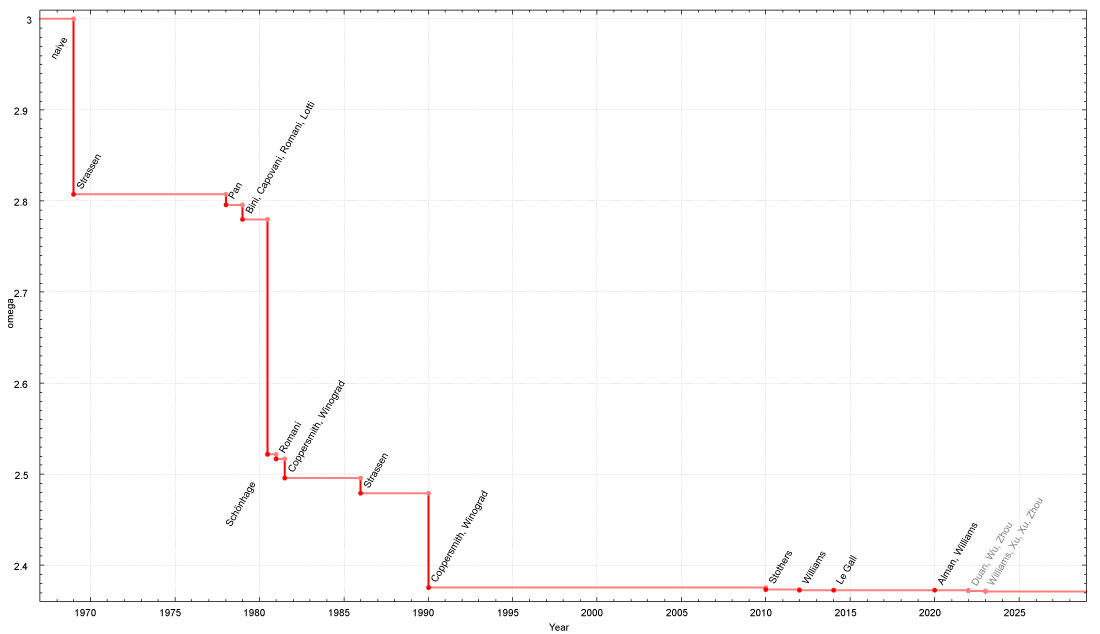
L’avantage est que la méthode triviale (ou méthode standard) pour effectuer cette opération est simple à réaliser à la main ou avec un ordinateur tant que la taille de la matrice reste raisonnable. L’inconvénient est que le nombre d’étapes de calcul nécessaires pour cet algorithme croît exponentiellement avec la taille de la matrice. « On peut compter ces additions et multiplications nécessaires pour multiplier deux matrices avec l’algorithme trivial. Pour une matrice avec n lignes et n colonnes, ce coût, appelé “complexité de l’algorithme”, est de n3 », explique Clément Pernet, enseignant-chercheur au Laboratoire Jean Kuntzmann3. Exemple : si deux matrices ont 1 000 lignes et 1 000 colonnes chacune, alors l’ordinateur (ou l’humain) doit faire 1 milliard d’opérations (soit 1 0003) pour réussir à les multiplier. « Or des matrices de ces tailles-là sont courantes dans les applications, notamment en machine learning », prévient François Le Gall.
À la conquête du meilleur algorithme
Dès les années 1960, mathématiciens et informaticiens se sont demandé si les matrices pouvaient être multipliées avec moins d’opérations. « Volker Strassen (mathématicien allemand, ndlr) s’était mis en tête que cela n’était pas possible. C’est pourtant lui qui a trouvé le premier un algorithme permettant de résoudre un produit de matrice en moins de n3 étapes », sourit Clément Pernet. Une découverte qui a lancé la quête de l’algorithme optimal du produit matriciel ! « La motivation principale est de faire des calculs rapides », souligne François Le Gall. Car multiplier deux matrices prend du temps : 30 secondes pour deux matrices de 10 000 lignes et 10 000 colonnes mais 4 minutes avec le double de lignes et de colonnes. Trouver un algorithme qui diminue le nombre d’étapes de calcul nécessaires permettrait de réduire le temps de calcul global. Une réduction d’autant plus sensible que la taille de la matrice augmente.
Comparons l’algorithme trivial à un hypothétique algorithme de multiplication dont la complexité serait n². Lors de la multiplication de deux matrices de taille 3 x 3, l’avantage de la seconde méthode par rapport à l’algorithme trivial n’est pas énorme. En revanche, si la taille de la matrice est d’un million de colonnes pour autant de lignes, le deuxième algorithme nécessitera un million de fois moins de calculs, soit un million de fois moins de temps et d’énergie dépensée. « Notre motivation théorique est aussi de comprendre jusqu’où on peut réduire la valeur de la puissance de n », expose François Le Gall. Ce que l’on sait, c’est que même optimisé, l’algorithme ne peut descendre sous une complexité de n2. En effet, n² est le nombre de cases qui composent la matrice résultat. Il faut donc au minimum n² étapes pour écrire le résultat. Pour faire baisser la complexité, les chercheurs concentrent donc leurs efforts sur la réduction du nombre de multiplications indispensables à réaliser avant la résolution d’un produit de matrices. « On connaît bien le nombre d’additions à faire et il est petit par rapport au nombre de multiplications. Alors c’est surtout ces dernières qui déterminent la puissance de n », éclaire François Le Gall.
Une complexité qui décroît « péniblement »
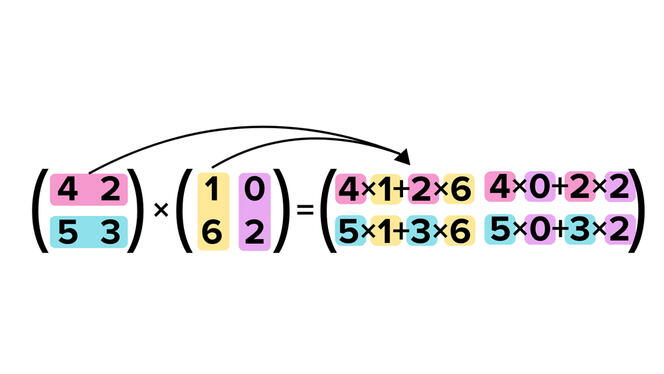
La première amélioration, l’algorithme de Volker Strassen, réduit la complexité de n3 à n2,807. Pour la construire, le mathématicien a utilisé la méthode qui consiste à diviser pour régner. L’idée est la suivante : on décompose le problème (ici la matrice) en plusieurs sous-problèmes (des parties de la matrice), puis eux-mêmes en d’autres sous-problèmes jusqu’à obtenir uniquement des matrices de taille 2 x 2. Il ne reste ensuite qu’à multiplier tous ces résultats entre eux pour trouver le résultat final. De cette manière, la multiplication de deux matrices de taille 2 x 2 demande une multiplication de moins que la méthode triviale, et la multiplication de matrices de taille 10 000 x 10 000 offre un gain de temps d’environ 28 %. « Après Volker Strassen, il n’y a pas eu de progrès pendant dix ans. Puis entre 1978 et la fin des années 1980, il y a eu une compétition énorme ! », s'exclame François Le Gall. Plusieurs petites améliorations sont découvertes, d’abord grâce à de nouveaux travaux de Volker Strassen, puis ceux de Shmuel Winograd et Don Coppersmith, tous deux mathématiciens. Avec une autre méthode de décomposition des matrices, ces derniers ont ainsi réussi à faire décroître la complexité jusqu’à atteindre n2,376.
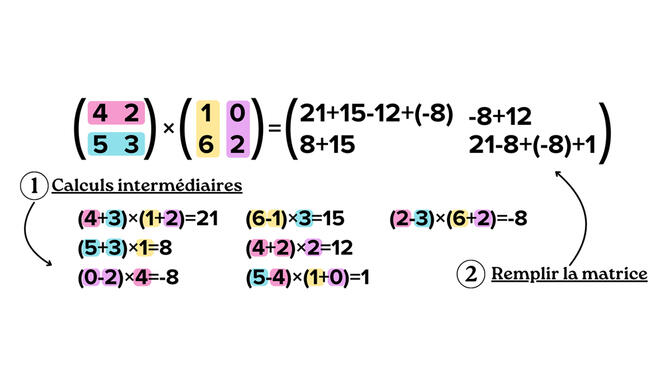
Depuis les années 2010, des progrès ont successivement été obtenus en améliorant cette méthode bien précise. La dernière optimisation en date a été réalisée par Zhou Renfei et ses collègues de l’Institut interdisciplinaire des sciences de l’information à l’université de Tsinghua (Chine) et, à la fin 2023, en passant l’exposant de 2.372860 à 2.371866. Un résultat qui ne paye pas de mine mais qui est mathématiquement déterminant. « Ils ont trouvé que quelque chose dans la méthode de Coppersmith et Winograd n’était pas optimal. On avait loupé ça », félicite François Le Gall.
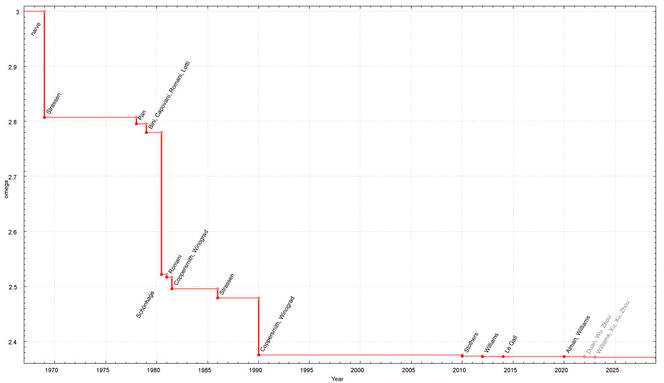
En chemin, la motivation théorique a pris le pas sur les améliorations réelles. « Après les années 1970, les algorithmes de multiplication matricielle sont devenus galactiques », prévient Clément Pernet. En d’autres termes, ces algorithmes sont si complexes qu’ils ne réduisent le temps de calcul que pour des matrices si gigantesques que tous les ordinateurs de la Terre ne suffiraient pas à les stocker. Alors, en pratique, ils ne sont jamais utilisés pour multiplier deux matrices, même avec des milliers de lignes et de colonnes. Pour autant, ce n’est pas parce que le résultat n’est pas utilisé, qu’il n’est pas intéressant. « Ces recherches permettent de répondre à des questions fondamentales et elles demandent de mettre en place de nouvelles techniques », pointe Gabriel Peyré. Cette course entre théoriciens pourrait bien déboucher sur des algorithmes plus rapides et utilisables dans des applications concrètes. ♦
Mots-clés
Partager cet article
Auteur
Charlotte Mauger est journaliste scientifique indépendante.
Voir aussi
Commentaires
"L’inconvénient est que le
Pierre Arnoux le 9 Juin 2024 à 01h39"Méthode triviale : lors de
Pierre Arnoux le 9 Juin 2024 à 01h42Connectez-vous, rejoignez la communauté
du journal CNRS