Vous êtes ici
Donner du sens à la mécanique quantique

Dans un article publié dans la revue Foundations of Physics1, vous présentez ce que vous appelez une « nouvelle ontologie » de la mécanique quantique. Que voulez-vous dire par là ?
Alexia Auffèves2 : Faire de l’ontologie consiste à s’intéresser à ce qui existe dans le monde, à la nature de la réalité contrairement à l’épistémologie, qui s’intéresse à ce qu’on peut connaître du monde. Mon amie philosophe Nayla Farouki me dit souvent que toute théorie physique devrait commencer par poser une ontologie, c’est-à-dire par énoncer des principes clairs sur la nature de la réalité physique, avant de poser le formalisme mathé-matique. C’est cet ordre des étapes : ontologie, puis formalisme, que nous souhaitons rétablir aujourd’hui, car, historiquement, la mécanique quantique n’a pas été construite ainsi.
veut replacer
la mécanique
quantique dans
le cadre du réalisme physique.
Philippe Grangier3 : Ce qui est curieux est que la mécanique quantique est une science extraordinairement précise, dont les prédictions ont toujours été vérifiées jusqu’à aujourd’hui. Mais pourtant son interprétation reste soumise à débat : différentes visions du monde s’opposent à son sujet. Beaucoup de physiciens ou de philosophes ont même dit que la mécanique quantique signifiait la mort du réalisme physique, d’une réalité extérieure à l’observateur, sur laquelle on peut acquérir des certitudes. Notre approche veut replacer la mécanique quantique dans le cadre de ce réalisme physique.
Qu’est-ce que la mécanique quantique a de si spécial pour que les physiciens aient encore besoin de s’interroger sur ses fondements près d’un siècle après sa naissance ?
P. G. : La mécanique quantique propose une description du monde très différente de celle de la physique dite classique. Le propre de la physique classique est d’isoler, au moins par la pensée, l’objet qu’on veut étudier, par exemple la Terre, une bille ou une particule, puis de mesurer ses propriétés. Pour cela, on pose des questions à l’objet sur sa masse, sa vitesse, son énergie… Autant de questions qu’on veut. Il faut bien sûr des appareils pour mesurer ces grandeurs. Mais, une fois leur valeur connue, on peut faire abstraction de l’appareil de mesure et considérer que ces grandeurs appartiennent en propre à l’objet. Elles constituent en quelque sorte sa carte d’identité, ce qu’on appelle en physique « l’état » du système. En mécanique quantique, il est notoire que cette vision des choses ne marche plus. Tous les physiciens sont d’accord sur cela. Mais en quel sens peut-on dire que cela ne marche plus ? C’est là que les avis divergent.
A. A. : Le côté « bizarre » de la mécanique quantique vient du fait que les résultats de mesure peuvent être aléatoires même si le système se trouve dans un état bien défini. Par exemple, un photon polarisé à 45° a une probabilité de 50 % de traverser un polariseur orienté verticalement (lire l’encadré ci-dessous). L’autre grande différence avec la physique classique est que l’ordre dans lequel est effectuée la mesure est déterminant en mécanique quantique. Classiquement, si je mesure la masse d’une table, puis sa couleur, j’obtiens les mêmes résultats que si j’observe d’abord sa couleur, puis sa masse. Ce n’est pas toujours vrai en physique quantique. Nos intuitions et nos habitudes sont mises à mal car, dans la vie de tous les jours, nos certitudes viennent du fait que nous obtenons toujours la même réponse à la même question. On explique cette répétabilité par une cause permanente qui est l’existence d’un état, appartenant au système tout seul, qui existe même si personne ne le regarde. Par exemple : la table est noire. En physique quantique, le système est toujours interfacé à un contexte expérimental dont on ne peut pas faire abstraction. Le système ne se livre jamais tout seul. Comment accéder alors à son état ?
Sur ce point, on entend souvent dire que c’est l’appareil de mesure qui perturbe le système…
A. A. : Oui. Quand j’ai commencé à apprendre la mécanique quantique, on m’a beaucoup parlé de l’expérience de pensée du microscope de Heisenberg. Lorsque j’observe un petit système, je dois l’éclairer avec de la lumière, autrement dit le bombarder de photons. Et donc si je connais sa position, je ne peux plus connaître sa vitesse car elle a été perturbée par les chocs avec les photons. Je n’arrive donc jamais à « attraper » l’état complet du système et c’est pour ça que la mécanique quantique est probabiliste. Mais je trouve cette explication frustrante, car elle fait de l’aléatoire une sorte de barrière qui apparaît sans que l’on sache pourquoi4 et surtout elle nous contraint à travailler avec des concepts (l’état du système) qui ne sont pas accessibles de façon simple.
œuvre humaine,
mais ce n’est pas
l’observateur qui
crée la réalité.
Quels sont les principes de base de votre nouvelle interprétation ?
P. G. : D’abord, nous avons une sorte de « postulat zéro » qui est le réalisme : la physique décrit un univers qui existe indépendamment de l’observateur et qui obéit à des règles intelligibles et universelles. La science est une œuvre humaine, mais ce n’est pas l’observateur qui crée la réalité.
A. A. : Ce qui constitue la réalité, ce sont des grandeurs physiques que l’on peut prédire de façon certaine, c’est-à-dire qu’on peut mesurer de manière sûre et répétable en retrouvant toujours le même résultat si on refait l’expérience. En physique classique, cela va de soi, car les propriétés que l’on mesure sont attribuées directement au système, le système étant simplement l’objet qu’on étudie : une particule, un ensemble de particules, etc. En physique quantique, le point fondamental que nous soulignons est qu’on ne peut pas oublier le contexte de la mesure, c’est-à-dire l’appareillage extérieur à l’observateur qui permet d’obtenir ces propriétés. Par exemple : quelle orientation du polariseur utiliser, ou quelle direction de champ magnétique appliquer, ou de quel détecteur se servir. Et en physique quantique, il y a bien aussi des résultats certains et répétables, mais à condition de considérer à la fois le système et son contexte. Prenons par exemple un photon comme système et un polariseur vertical comme contexte. Pour nous, le photon tout seul n’a pas de polarisation (lire l’encadré ci-contre). Mais l’ensemble photon et polariseur a une polarisation. Si je vous donne mon photon et que vous le faites passer par un polariseur vertical, vous trouverez le même résultat que moi. Cet état quantique, que nous appelons « modalité », appartient à la fois au système et au contexte. C’est notre premier postulat.
———————————————————————————————
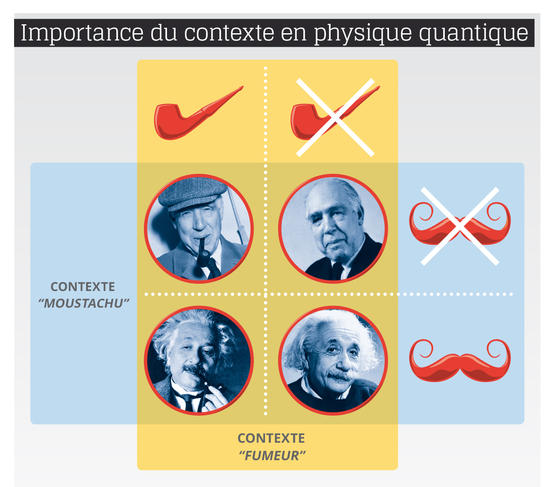

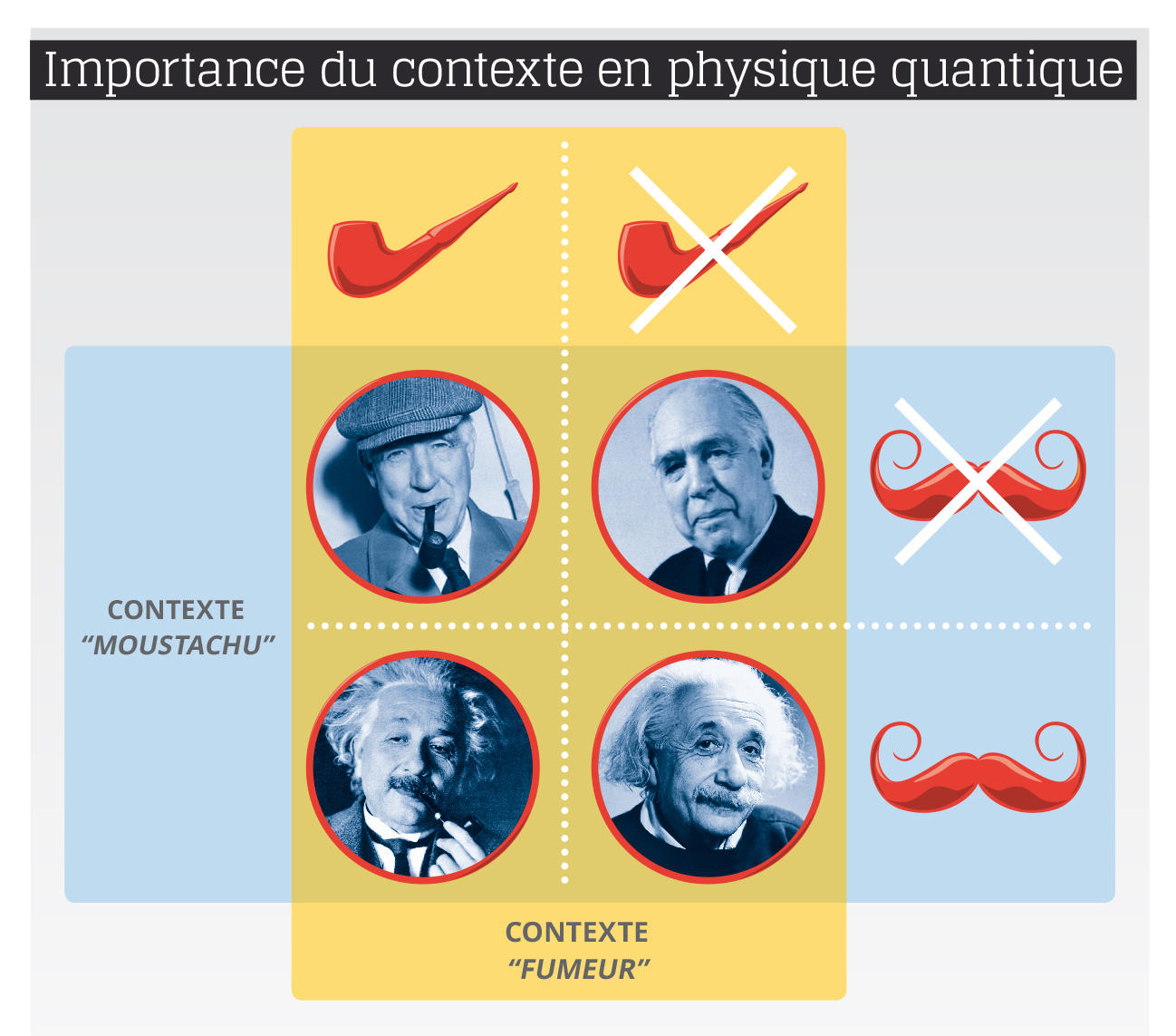
Légende : En physique classique, on peut combiner deux propriétés, comme fumer la pipe ou pas, et être moustachu ou pas, pour obtenir quatre situations possibles. En physique quantique, pour la polarisation d’un photon par exemple, on doit choisir un contexte, dans lequel on ne peut avoir que deux réponses possibles, relatives soit à une propriété, soit à l’autre. Cette quantification binaire (une réponse parmi deux) interdit ainsi de savoir si un fumeur de pipe est moustachu ou pas : si on rencontre un moustachu, puis qu’on apprend qu’il fume la pipe, il se peut qu’en le regardant à nouveau on constate qu’il n’a plus de moustache ! La « modalité » (l’état quantique) appartient à la fois au système quantique, qui répond par oui ou non, et au contexte classique qui définit la question, c’est-à-dire la propriété physique qui est mesurée.
———————————————————————————————
On peut donc accéder à la réalité, qui appartient à la fois au système et au contexte, avec certitude. Mais pourquoi les probabilités interviennent-elles en mécanique quantique ?
P. G. : Parce que la mécanique quantique est justement quantique, c’est-à-dire « quantifiée » : le nombre de modalités d’un ensemble « système et contexte donnés » est fini. C’est notre second postulat. Dans l’exemple du photon et du polariseur vertical, il n’y a que deux modalités possibles : soit le photon est transmis, soit le photon est réfléchi par le polariseur vertical. Une fois que je connais cette modalité, par exemple le photon est transmis, celle-ci est certaine : l’ensemble « photon et polariseur » est polarisé verticalement, et j’obtiens le même résultat quand je répète la mesure. Mais la carte d’identité que je peux dresser est limitée. Je ne peux pas demander des détails au photon. Si je veux la réponse à d’autres questions, il faut que je change de contexte, par exemple en tournant l’orientation du polariseur à 45°. J’ai alors accès à deux autres modalités, soit le photon est transmis, soit le photon est réfléchi par le polariseur à 45°, mais ces modalités ne s’ajoutent pas aux deux modalités précédentes, sinon cela contredirait notre second postulat, nous pourrions « extorquer » des détails au photon. Je ne sais donc pas de manière certaine quel sera le résultat de la nouvelle mesure, mais seulement sa probabilité : sachant que le photon a été transmis par un polariseur orienté verticalement, il a telle probabilité (ici, 50 %) de traverser un polariseur orienté à 45°. Les probabilités en mécanique quantique servent donc à relier les résultats de mesures effectuées dans des contextes expérimentaux différents. Après avoir effectué une mesure avec le polariseur à 45°, si je veux revenir avec un polariseur vertical, il faut à nouveau changer de contexte : le résultat sera à nouveau probabiliste et je n’obtiendrai pas forcément le même résultat qu’au début. Cela explique pourquoi l’ordre des mesures est déterminant en physique quantique.
A. A. : Le nombre de réponses (de modalités) que peut fournir un système macroscopique classique n’est pas limité et je peux compléter sa carte d’identité autant que je veux. À l’opposé, l’aléatoire en mécanique quantique vient de la mise en contact d’un très petit système, qui ne peut donner qu’un nombre fini, quantifié de réponses, et d’un gros contexte classique, qui peut poser une infinité de questions. L’aléatoire apparaît donc comme une caractéristique essentielle, ontologique, de la théorie quantique, contrairement à l’interprétation du microscope de Heisenberg, où l’aléatoire est une conséquence d’un problème pratique. De plus, ici, le caractère aléatoire découle essentiellement de la quantification. Cela replace la quantification au cœur de la théorie quantique.
Quelles sont les autres implications de cette relecture de la physique quantique ?
P. G. : Il y a un prix à payer quand on dit que la réalité appartient simultanément à un objet et à un contexte. Cela revient à dire que la réalité est bipartite : d’un côté le système, de l’autre le contexte, et le premier ne peut pas se donner sans le second. C’est en quelque sorte une nouvelle définition de la réalité. L’implication profonde est qu’on ne peut plus imaginer le monde comme construit à partir du bas, à partir de particules qui « posséderaient » chacune un état défini. La vision naïve selon laquelle l’accumulation des particules microscopiques crée les objets macroscopiques ne fonctionne pas dans notre approche car, pour parler des particules et définir leur état, j’ai déjà besoin d’un contexte macroscopique et je ne peux pas attendre qu’il émerge du monde microscopique.
Dans votre interprétation, que deviennent les paradoxes qu’on cite souvent, comme celui du chat de Schrödinger, à la fois mort et vivant ?
P. G. : Pour pouvoir parler d’un chat « mort et vivant », il faudrait disposer d’un contexte où cet état apparaîtrait comme une modalité certaine et reproductible. Autant il existe un contexte où on peut observer le chat soit dans l’état « vivant », soit dans l’état « mort », autant il n’existe aucun contexte où l’on pourrait observer un chat « mort et vivant » : on peut écrire une formule mathématique, mais on ne peut lui associer aucune propriété physique mesurable. Pour nous, cet état n’a donc aucune réalité physique. Remarquons par contre que pour des systèmes « mésoscopiques » impliquant un petit nombre de particules quantiques (jusqu’à une centaine actuellement), on peut construire de telles superpositions, que les physiciens appellent des « chatons de Schrödinger. » De façon générale, dans notre approche, un vrai état (une modalité) n’est jamais défini de manière abstraite : il doit correspondre à une expérience certaine et reproductible, pour un système et un contexte donnés.
A. A. : En fait, le problème du chat de Schrödinger est essentiellement lié à la notion de superposition cohérente en mécanique quantique : que signifie « être dans deux états à la fois » ? Dans notre interprétation, cela n’a pas de signification intrinsèque, mais cela veut juste dire qu’il existe un contexte qui va donner une mesure certaine. Par exemple, on ne dit pas d’un photon à 45° qu’il est « à la fois » dans l’état 0° et dans l’état 90° en criant au mystère. Cela signifie juste que si j’oriente le polariseur à 45°, le photon sera transmis avec certitude. Pour le photon, ce comportement de superposition existe parce que la modalité appartient à la fois au système et au contexte, et qu’on peut changer de contexte en tournant le polariseur. Il n’existe rien de tel pour la vie et la mort du chat.
Comment réagissent vos collègues quand vous leur présentez votre vision des choses ?
P. G. : Nous avons présenté notre point de vue dans plusieurs conférences, grandes et petites. J’ai l’impression que cela ébranle les physiciens sur le moment, puis qu’ils reviennent à leur routine. Mais un des principes de la pédagogie est qu’il faut répéter avant d’être bien compris…
A. A. : Nos présentations se passent de mieux en mieux. Nos images sont plus claires désormais. Mais beaucoup de physiciens sont rétifs à cette idée, car ils ont tendance à penser que l’état quantique doit être attribué à un système tout seul. Au contraire, quand on dit au grand public non spécialiste que les propriétés dépendent à la fois du système et du contexte, cela semble assez évident. Il y a une petite différence de perception entre les physiciens et le reste du monde.
physiciens sont
rétifs à notre point
de vue, car ils
ont tendance
à penser que l’état
quantique doit être
attribué à un
système tout seul.
P. G. : Quand nous attribuons la réalité quantique en même temps à un objet et à un contexte, c’est un peu comme monsieur Jourdain et sa prose : beaucoup de chercheurs font cela, mais sans en avoir conscience. Cependant, beaucoup ne sont pas prêts à l’admettre, car ils sont très attachés au fait d’attribuer un état uniquement à un système. Tout le monde est d’accord pour dire que la mécanique quantique est ontologiquement différente de la physique classique, mais j’ai l’impression que la majorité de nos collègues tiennent à conserver cet aspect classique, celui qui pose justement problème d’après nous ! Après, certains ne partagent pas la nouvelle définition de la réalité qu’implique notre approche. Donc pour l’instant, notre interprétation ne fait pas du tout l’unanimité, sans doute aussi parce que la plupart des collègues qui ont réfléchi à ces questions se sont forgé leur propre interprétation et qu’ils n’en changeront pas sans une très bonne raison.
A. A. : Je pense que ces réticences viennent profondément de la façon très mathématique et formelle dont la mécanique est enseignée. Dès le départ, il y a un parti pris : les états sont attribués au système. Il est ensuite difficile d’aller contre nos premières intuitions construites avec les mathématiques.
P. G. : J’enseigne la mécanique quantique à l’École polytechnique selon la méthode « traditionnelle » en suivant de près la façon dont la théorie s’est construite historiquement. On ne part pas des mathématiques, mais des photons d’Einstein pour les ondes lumineuses, puis des interférences avec des particules et de leur interprétation grâce aux ondes de De Broglie. Au début, cette onde apparaît forcément comme une espèce d’onde électromagnétique, ou une onde à la surface de l’eau… une « vraie » onde. Puis on explique assez rapidement que ce n’est pas une « vraie » onde, mais une amplitude de probabilité, donc un outil de calcul des résultats possibles. Mais alors il est difficile de se détacher d’une vision où l’onde est « quelque chose » ; et si elle n’est pas « quelque chose », de quoi parle-t-on, puisque les physiciens eux-mêmes ne semblent pas parvenir à répondre à cette question ? Parvenir à maîtriser ces notions fait partie de l’apprentissage de la physique quantique. Dans notre approche, la réalité est dans les quantités qu’on va mesurer, mais comprendre le sens de cette affirmation n’est certainement pas immédiat non plus.
Y a-t-il des liens entre ces réflexions fondamentales et votre travail de recherche plus quotidien, en laboratoire ?
P. G. : Si on regarde les résultats anciens et récents sur les tests des inégalités de Bell, on voit que les questions sur la nature et le rôle de l’intrication quantique sont en un certain sens à l’origine d’un champ de recherche très actif, l’information et la cryptographie quantiques. Ce que nous faisons tous les jours relève plutôt de ce domaine. Mais au départ, le test de Bell était conçu pour trancher un débat philosophique sur la nature de la réalité. Une réponse expérimentale convaincante a été apportée à la question posée, mais elle ne clôt pas le débat philosophique et métaphysique, et nos réflexions s’inscrivent dans ce contexte. Nous ne faisons donc pas de la pure métaphysique, et nous ne voulons pas nous arrêter là, sinon, on pourrait dire que nous ne formulons que des "pétitions de principe", que Niels Bohr avait déjà plus ou moins dit la même chose, etc. Notre objectif est donc d’établir un lien plus étroit entre nos postulats et le formalisme mathématique, c’est-à-dire expliquer pourquoi, une fois posée la quantification du nombre de modalités d’un système et d’un contexte, on aboutit à la formulation mathématique usuelle de la physique quantique. Notre démarche ne conduit pas, pour l’instant, à des prédictions différentes de celles de la mécanique quantique standard, et la possibilité de trancher entre notre approche et une autre (par exemple au moyen de tests expérimentaux, comme on a pu le faire avec les inégalités de Bell) reste un problème ouvert.
———————————————————————————————
Questions de polarisation
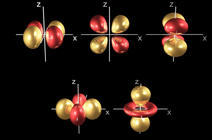
Avec la fréquence d’oscillation (qui détermine la couleur) et la direction de propagation, l’angle de polarisation est la troisième propriété intrinsèque d’une onde électromagnétique comme la lumière. La lumière naturelle est souvent « non polarisée » ce qui veut dire que tous les angles de polarisation (et toutes les couleurs) sont également présents. Toutefois, quand elle interagit avec de la matière – en passant par exemple à travers un polariseur –, certaines directions de polarisation seront privilégiées. La lumière et les photons qui la composent deviennent alors « polarisés ». Quand deux photons sont intriqués, l’angle de polarisation de l’un est fortement corrélé avec celui de l’autre, quelle que soit la distance entre les deux photons.
- 1. « Contexts, Systems and Modalities : A New Ontology for Quantum Mechanics », Alexia Auffèves et Philippe Grangier, Foundations of Physics, publié en ligne le 21 septembre 2015. DOI 10.1007/s10701-015-9952-z
- 2. Institut Néel du CNRS.
- 3. Laboratoire Charles Fabry (CNRS/Institut d’optique Graduate School/Univ. Paris Sud).
- 4. En physique classique, le fait de prendre une mesure peut aussi perturber les résultats, mais on peut corriger cette perturbation ; ce n’est plus le cas en physique quantique.
Voir aussi
Auteur
Sylvain Guilbaud, né en 1986, est journaliste scientifique. Ingénieur de formation, il est diplômé de l’École supérieure de journalisme de Lille et anime le blog http://madosedescience.wordpress.com.