On pourrait penser que mathématiques et valorisation ne vont pas forcément de pair. Comment voyez-vous le lien entre les deux ?
Albert Cohen1 : La preuve n’est plus à faire que les mathématiques sont à l’origine d’avancées techniques très concrètes. En revanche, la valorisation ne peut pas être une fin en soi. L’une des grandes forces de cette discipline est précisément de prendre du champ par rapport à une application spécifique pour essayer de dégager des principes sous-jacents qui permettraient de résoudre ces problèmes, mais aussi de nombreux autres problèmes.

Voyez-vous alors une différence entre des maths « pures », fondamentales, et des maths appliquées, tournées vers la valorisation ?
A. C. : Personnellement, en tant que mathématicien appliqué, je me pose régulièrement la question de la pertinence de l’objet de mes recherches pour des applications et je vais puiser des problèmes chez les ingénieurs, les physiciens, les biologistes pour nourrir une réflexion mathématique plus fondamentale. Cela étant dit, je pense qu’il n’existe pas de frontière entre mathématiques pures et appliquées.

Est-ce à dire que l’idée de valorisation préexiste déjà en amont de vos recherches mathématiques ou se révèle à la suite d’une avancée théorique ?
A. C. : La question ne se pose jamais en des termes aussi tranchés. Mes premiers travaux portaient sur la théorie des ondelettes. C’était un sujet en ébullition, à un carrefour entre l’analyse numérique, l’analyse harmonique et d’autres disciplines comme le traitement du signal et de l’image, la physique de la turbulence. Il y a des allers-retours permanents entre les questions fondamentales et appliquées. Je n’ai jamais eu l’impression de partir de l’un pour aller vers l’autre, mais plutôt d’être immergé dans un environnement qui nourrit les réflexions de tous les côtés.

C’est donc ce qui s’est produit avec les ondelettes ?
A. C. : Les ondelettes ont été découvertes par un ingénieur, Jean Morlet, qui étudiait le traitement du signal sismique pour la prospection pétrolière. Des physiciens théoriciens, autour d’Alex Grossmann, puis des mathématiciens, autour d’Yves Meyer, d’Ingrid Daubechies et de Stéphane Mallat2, ont fait le lien entre ces idées et des formules de représentations en théorie des groupes, des techniques d’analyse harmonique, ainsi que des méthodes de filtrage numérique. Les ondelettes sont un outil mathématique. Elles permettent de décomposer des fonctions arbitraires pour analyser plus finement leurs propriétés locales. Mes travaux avec Ingrid Daubechies et Jean-Christophe Fauveau ont permis d’identifier une nouvelle classe d’ondelettes, qui a ensuite été adoptée par les ingénieurs pour compresser des images. Mais nous ne nous sommes pas demandé a priori : « Comment faire pour créer un nouveau format de compression ? » Je pense que si nous nous étions posé cette question, nous ne serions pas arrivés à une solution aussi élégante.

Reconstruction d’un champ acoustique (à g.) à l’aide d’une méthode classique (au milieu), puis grâce au concept de parcimonie (à d.).

Reconstruction d’un champ acoustique (à g.) à l’aide d’une méthode classique (au milieu), puis grâce au concept de parcimonie (à d.).

G. CHARDON/ANR ECHANGE

G. CHARDON/ANR ECHANGE

Partager

Partager

Ce nouveau format de compression a donc été adopté internationalement ?
A. C. : Oui, il s’agit du format Jpeg 2000, utilisé chez les professionnels de l’image essentiellement. L’intensité lumineuse change peu d’un point à l’autre d’une image, sauf au niveau des contours des objets. Quand on la décompose sur une base d’ondelettes appropriée, très peu de coefficients vont donc avoir une valeur importante et la plupart seront presque nuls, ce qui permet la compression. Contrairement au format Jpeg, très répandu sur le Web, le format Jpeg 2000 ne « découpe » pas l’image en bloc et crée donc moins d’artefacts visuels.

Par exemple ?
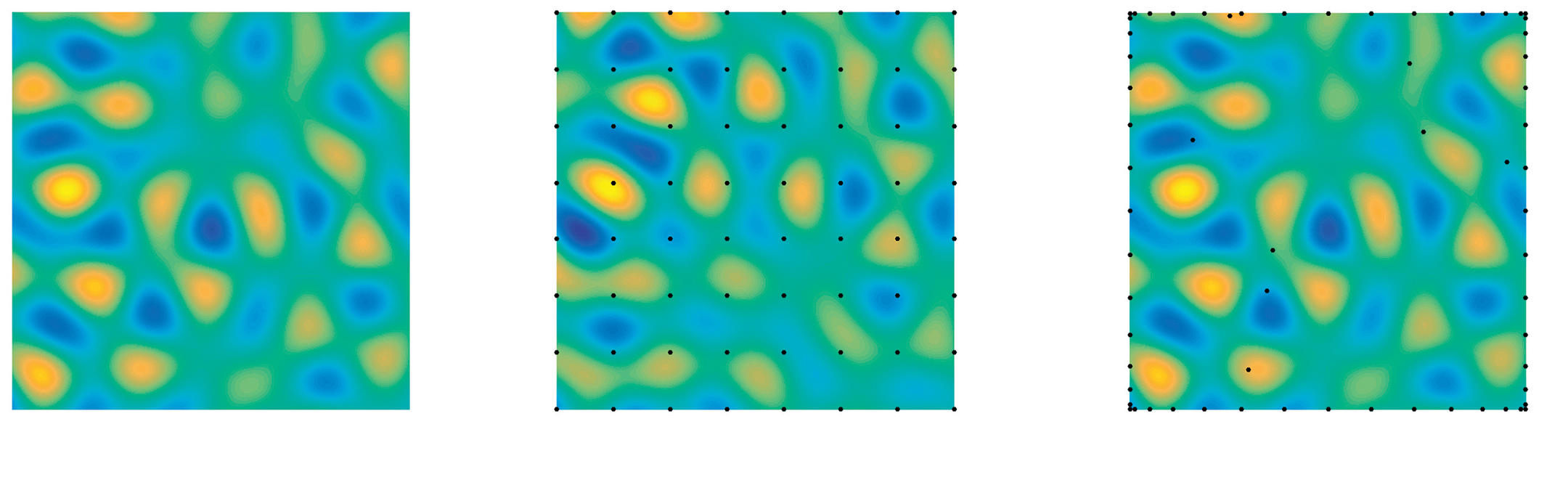
A. C. : Dans la simulation numérique de certains phénomènes physiques, tels que les écoulements fluides, l’information importante se concentre dans des régions localisées, par exemple là où se produisent des ondes de choc. On peut développer des méthodes qui tirent parti de ces propriétés. Depuis dix ans, le domaine du compressed sensing (échantillonnage compressif) a connu un développement spectaculaire autour des travaux d’Emmanuel Candès et de David Donoho. L’enjeu principal est ici de capturer des signaux à partir d’un très petit nombre de mesures bien choisies et de les reconstruire avec précision en utilisant leurs propriétés de parcimonie dans une représentation connue. En lien avec ces idées, j’ai collaboré avec des acousticiens sur la disposition optimale d’un nombre donné de micros dans une pièce pour reconstruire l’ensemble d’un champ acoustique. Plus récemment, j’ai appliqué ce concept à des fonctions qui dépendent d’un grand nombre de variables, et dont l’approximation numérique est inconcevable par des méthodes classiques. Les ingénieurs sont naturellement confrontés à ces problèmes lorsqu’ils cherchent à comprendre la dépendance de phénomènes – qu’ils soient expérimentaux ou simulés numériquement –, en fonction de nombreux paramètres physiques. Le concept de parcimonie peut aider à surmonter cette « plaie des grandes dimensions ».

La valorisation est-elle également une source de financement de vos recherches ?
A. C. : Personnellement, je bénéficie à la fois d’un financement européen, via une bourse ERC, et du dispositif de l’Institut universitaire de France. Il s’agit donc de fonds publics. Même si certains de mes résultats ont été valorisés et ont eu des applications commerciales – mon nom figure sur deux brevets – le passage d’une idée à une réalisation technologique concrète est un processus long et complexe, et je n’ai pas vocation à le suivre jusqu’au bout. Je n’ai jamais cherché à utiliser ce moyen comme source de financement. Ce qui reste à mon sens fondamental dans la recherche, c’est la liberté complète du scientifique. Y compris celle de s’égarer en dehors des sentiers que lui imposerait un impératif de valorisation. La plupart des avancées technologiques n’auraient pas eu lieu sans cette errance vertueuse des chercheurs et, en particulier des mathématiciens.

À lire aussi :
Les maths dopent l'économie française
Maimosine met le monde en modèles

Pour en savoir plus :
L'ICIAM 2015 (Congrès International de Mathématiques Appliquées et Industrielles) se tient du 10 au 14 août à Beijing, en Chine.