Vous êtes ici
La plus grosse preuve de l’histoire des mathématiques

Il faudrait 10 milliards d’années à un être humain pour la lire. D’une taille phénoménale de 200 téraoctets – soit l’équivalent de tous les textes numérisés détenus par la bibliothèque américaine du Congrès –, c’est la plus grande preuve mathématique jamais produite. Trois informaticiens américano-britanniques viennent d’annoncer l’avoir établie grâce à un supercalculateur1. Leurs travaux seront présentés au cours de la conférence internationale SAT, qui se tiendra à Bordeaux du 5 au 8 juillet prochains.
Un problème trentenaire résolu en force
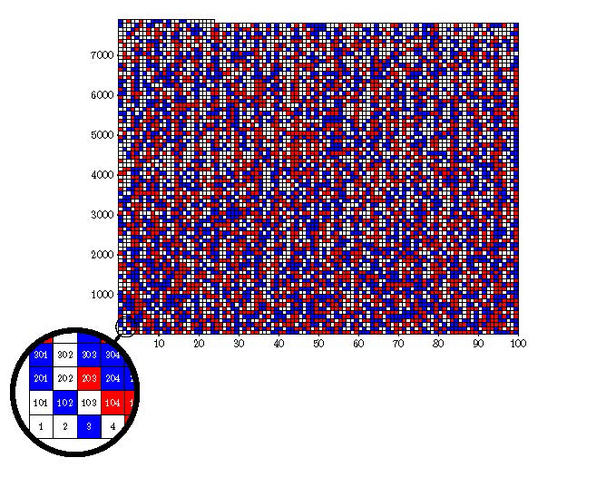
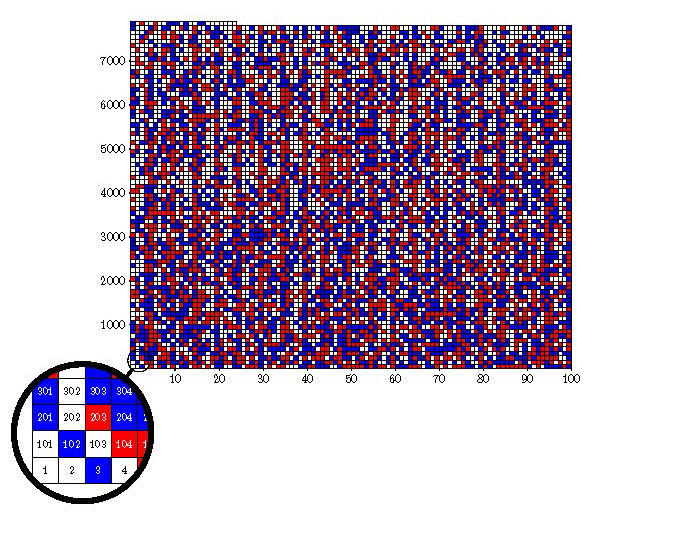
Le problème qu’ont résolu les trois chercheurs et qui a nécessité une preuve aussi longue est celui dit de la « bicoloration des triplets de Pythagore ». Resté sans réponse depuis les années 1980, ce problème simple en apparence pose la question suivante : est-il possible de colorier chaque entier positif en bleu ou en rouge de telle manière qu’aucun triplet d’entiers a, b et c qui satisfait la fameuse équation de Pythagore a² + b² = c² soient tous de la même couleur ? Par exemple, pour le triplet 3, 4 et 5, si 3 et 5 sont coloriés en bleu, alors 4 doit être rouge.
À cette énigme, le trio d’informaticiens a répondu non. Ils ont montré que, jusqu’à 7 824, il est possible de colorier ainsi les entiers, et même de plusieurs façons mais, arrivé à 7 825, cela devient impossible. « Pour le prouver, les chercheurs n’ont pas eu d’autres choix que d’y aller “en force” en énumérant et en vérifiant toutes les combinaisons possibles », explique Laurent Simon, du Laboratoire bordelais de recherche en informatique2.
Une preuve inhumaine
Une tâche hors de portée pour un humain mais accessible à un ordinateur. Rendez-vous compte : il y a plus de 102300 façons de colorier les entiers jusqu’à 7 825 ! Heureusement, en tirant parti des différentes symétries du problème et en utilisant diverses techniques issues de la théorie des nombres, les chercheurs sont parvenus à réduire le nombre de possibilités à étudier à 1 000 milliards. « L’astuce de l’équipe a ensuite été de découper tous ces cas possibles en un million de paquets différents pour pouvoir résoudre le problème plus facilement », précise Daniel Le Berre, du Centre de recherche en informatique de Lens (Cril)3.
Il aura fallu alors deux jours au supercalculateur Stampede de l’université du Texas et à ses 800 processeurs pour passer en revue toutes ces possibilités et apporter la preuve tant attendue, générant pour cela 200 téraoctets de données. « Les chercheurs ont ensuite vérifié la preuve, trop longue pour être relue par un humain, en utilisant un autre programme informatique indépendant », précise Laurent Simon.
Désormais, les ordinateurs sont devenus des alliés indispensables aux mathématiciens pour résoudre ce genre de problème dit combinatoire. Déjà, en 2014, une preuve de 13 gigaoctets – c’était le record précédent – construite par ordinateur avait permis de mettre fin à une énigme similaire à celle des triplets de Pythagore.
La révolution des solveurs SAT
La raison de cette petite révolution ? C’est la mise au point par les informaticiens de nouveaux algorithmes très efficaces pour résoudre ces problèmes : les « solveurs SAT ». Dans le langage informatique, SAT signifie « satisfiabilité ». Il s’agit d’un formalisme logique qui capture toute la difficulté d’un problème combinatoire pour tenter ensuite de le satisfaire. Prenez un jeu de Sudoku ou un démineur, ce sont là deux exemples très simples de problèmes qui peuvent être appréhendés et résolus très facilement par ce formalisme.
En quinze ans, les informaticiens ont accompli des progrès considérables dans ce domaine. « Si bien que les solveurs SAT, cantonnés au départ à l’informatique théorique, ont vu leur utilisation exploser et ont permis de résoudre des problèmes de plus en plus difficiles », confie Daniel Le Berre. Aujourd’hui, Microsoft fait appel à ces algorithmes pour tester ses nouveaux systèmes d’exploitation. Il s’agit alors d’identifier une succession d’instructions parmi des millions susceptibles de causer un bug dans le logiciel ou au contraire de prouver qu’il n’y en aura pas. Même chose pour Intel qui vérifie grâce à ces outils le bon fonctionnement de ses microprocesseurs. Et le nombre d’applications ne cesse de croître en robotique, en bio-informatique ou encore en cryptographie.
D’autres preuves à venir…
Aujourd’hui, c’est au tour des mathématiques, donc, d’être touchées par cette vague. Ainsi, pour établir la preuve du problème des triplets de Pythagore, le trio d’informaticiens a utilisé le solveur baptisé Glucose, développé par Laurent Simon et Gilles Audemard du Cril. En 2014 aussi, c’est Glucose qui avait permis de construire ce qui constituait alors la plus longue preuve mathématique.
Et cette tendance ne semble pas près de s’arrêter. « Ce dernier résultat montre qu’il est possible de s’attaquer avec cette méthode à des problèmes mathématiques combinatoires extrêmement difficiles, pour lesquels aucune approche classique à la main n’est encore disponible, confie Laurent Simon. Il préfigure probablement la fin d’autres conjectures similaires qui résistent encore aujourd’hui aux mathématiciens. »
Voir aussi
Auteur
Julien Bourdet, né en 1980, est journaliste scientifique indépendant. Il a notamment travaillé pour Le Figaro et pour le magazine d’astronomie Ciel et Espace. Il collabore également régulièrement avec le magazine La Recherche.