Vous êtes ici
Claire Voisin, la conquête de l’algébrique
Temps de lecture : 8 minutes
Spécialiste de géométrie algébrique, directrice de recherche au CNRS à l’Institut de mathématiques de Jussieu jusqu’en juin dernier, désormais professeur au Collège de France, Claire Voisin, 54 ans, pourrait philosopher sur son métier pendant des heures. D’ailleurs, c’est avec la philo qu’elle a d’abord accroché au lycée. À l ‘époque, la poésie occupe aussi son esprit. Les maths, en revanche, n’ont pas d’emblée obtenu ses faveurs même si cela viendra assez vite.
À force de chercher, en compagnie de son père polytechnicien, les mille implications des théorèmes de base de la géométrie plane, tels ceux de Thalès ou Pythagore, à force de dévorer, dès l’âge de 15 ans, des livres de maths « qui traînaient à la maison ». Le chômage soudain du père de famille lui vaut de recevoir une bourse d’État pour poursuivre ses études. Après deux années de classes préparatoires, où les mathématiques deviennent enfin assez intrigantes à son goût, elle entre à l’ENS en 1981, à 19 ans. « J’avais un salaire, c’était formidable ! Ce salaire, je l’ai pris comme un message qui signifiait : on est content que vous fassiez des études, profitez-en ! »
Réconcilier l’algèbre et la géométrie
Agrégée de mathématiques dès 1983, elle soutient sa thèse trois ans plus tard, sous la direction d’Arnaud Beauville. Puis elle est aussitôt recrutée au CNRS. Au sein de l’institution, elle multiplie les exploits de carrière. Elle est élue membre de l’Académie des sciences en 2010 et est la lauréate de nombreux prix prestigieux, dont celui de la Société mathématique européenne en 1992. L'année 2016 aura été particulièrement riche : le 14 décembre, elle reçoit ainsi la médaille d'or du CNRS, la plus haute récompense scientifique française, quelques mois après être devenue la première mathématicienne à entrer au Collège de France où elle occupe la chaire de géométrie algébrique.
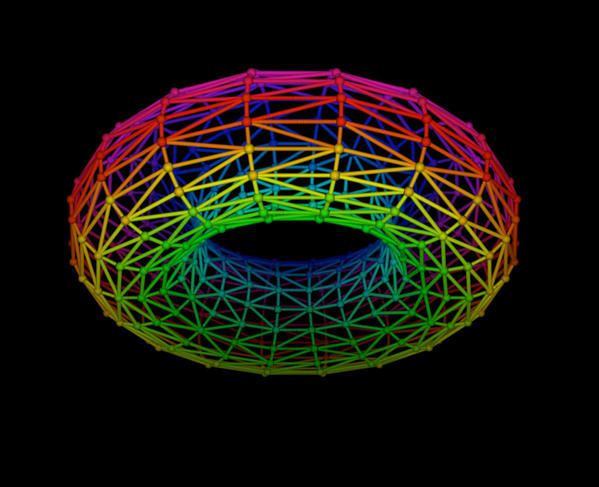
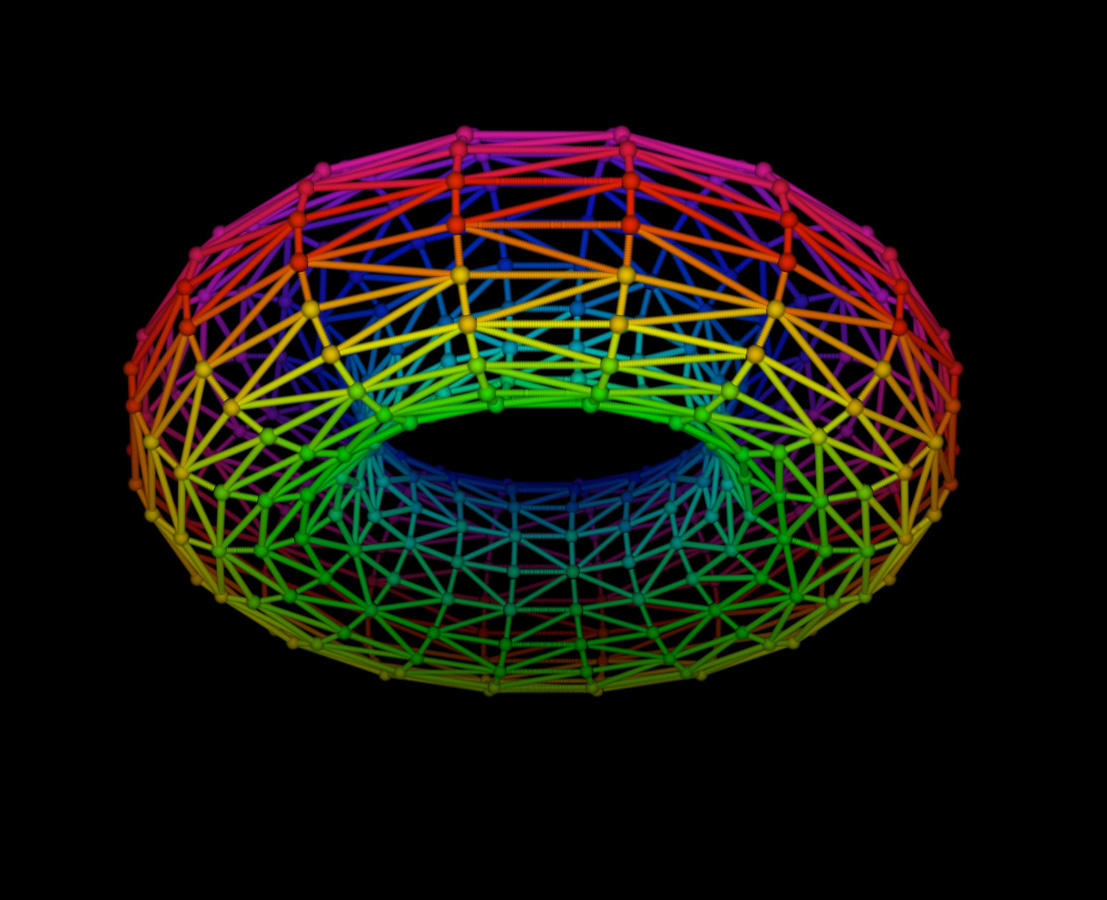
Devant notre difficulté à saisir en quoi consiste exactement cette discipline de haute voltige, elle file au tableau et dessine un grand tore qu’elle encadre d’une abscisse et d’une ordonnée. « À première vue, indique-t-elle, tout ce que l’on voit ici, c’est une sorte de bouée, avec un ou plusieurs trous au milieu. Mais en mathématique, on cherche à en savoir plus : comment les courbes tracées sur ce tore se coupent-elles ? Par quelles familles de courbes peut-on le recouvrir ? Peut-on le déplier et le superposer sur une sphère ? Ce sont là des questions de topologie et des outils, tels que la théorie de Morse ou la théorie de Hodge, permettent de les attaquer. Ces objets sont aussi définis par des équations algébriques complexes et cela donne d’autres façons de les étudier. »
« Ce qui est intéressant en géométrie algébrique, ajoute François Charles, professeur à l’université Paris-Sud à Orsay, ancien doctorant de Claire Voisin, c’est que l’on peut à la fois faire de la géométrie pour comprendre des équations algébriques et faire de l’algèbre pour comprendre des figures géométriques, il y a un va-et-vient permanent entre les deux approches. Mais cela nous pose aussi un problème : si l’algèbre et la géométrie nous éclairent chacune à leur façon pour comprendre un objet, nous ne parvenons pas toujours à faire le lien entre les deux, à les réconcilier », un peu comme les physiciens ne parviennent pas à lier dans une même théorie du tout les quatre forces fondamentales de l’Univers, qui le décrivent chacune à leur manière : la gravité d’une part, et la force électromagnétique, la force nucléaire faible, la force nucléaire forte de l’autre.
Une approche créative
Découvrir les arcanes de l’Univers, voilà qui parle à tout le monde ou presque. Mais disséquer mathématiquement un tore ou une sphère… à quoi ça sert ? À la question volontairement provocante, elle répond par un vif dithyrambe, qui laisse entrevoir toute la passion qu’elle voue aux mathématiques. « Ce sont des mathématiciens qui, dès l’Antiquité, ont calculé le rayon de la Terre ! plaide-t-elle. Les développements de la physique ne seraient pas possibles sans les mathématiques. C’est grâce aux mathématiques que l’on étudie la structure de l’Univers ! Tous les puissants outils théoriques que nous développons trouveront tôt ou tard une application. »
L’un de ses résultats les plus marquants est en relation avec le théorème de Kodaira. Elle a aussi montré l’impossibilité d’étendre la conjecture de Hodge au cadre kählérien. Elle a en outre travaillé en géométrie projective, montrant la conjecture de Green pour les courbes génériques par une construction inattendue et des calculs complexes. Ses travaux actuels sur les invariants birationnels sont très remarqués et ont été discutés le 5 novembre dernier, lors du séminaire Nicolas Bourbaki, l’une des plus célèbres « institutions » contemporaines de mathématiques.
« Je ne vais pas me prendre pour une artiste, mais il est vrai qu’il faut être créatif pour faire de bonnes mathématiques. D’ailleurs, j’ai beaucoup peint jusqu’à l’âge de 25 ans, révèle-t-elle en montrant deux toiles de sa confection accrochées dans son salon, et puis j’ai arrêté : notre métier monopolise beaucoup nos facultés de création ».
Quand elle était plus jeune, dès que l’un de ces problèmes se posait à elle, elle s’asseyait tout de suite à un bout de table pour tenter de le résoudre. Aujourd’hui, cela n’est plus toujours possible : Claire Voisin a de multiples responsabilités, des collègues, des étudiants et... cinq enfants, ainsi qu’une petite-fille. Alors, dans le brouhaha du quotidien, elle consigne chacune de ses réflexions dans un petit carnet – qu’elle extirpe d’une pile de documents posés au sol – et s’y replonge quand le calme revient.

« Nous disposons d’institutions remarquables qui contribuent au rayonnement des mathématiques françaises dans le monde. Malheureusement, les maths sont un peu malmenées au collège et au lycée : on en fait une discipline de sélection, ce qui peut avoir tendance à faire émerger surtout des gens arrogants. Il est aussi regrettable de ne transmettre aux élèves qu’une combinaison de définitions, de propriétés, de théorèmes, qui donne une idée figée de la discipline. Je serais en faveur d’un enseignement plus ouvert, qui donne accès à des maths qui ne soient pas faites à l’avance et pousse les élèves à se poser davantage de questions. »