Jean-Bernard Lasserre à la quête de l’optimum

14.03.2022, par

Angélique Le Touze

Jean-Bernard Lasserre au Laboratoire d’analyse et d’architecture des systèmes en février 2022.

Le grand prix Inria – Académie des sciences 2021, décerné à Jean-Bernard Lasserre pour distinguer l’ensemble de sa carrière, est l’occasion de revenir sur le parcours de ce chercheur à l'origine d'une nouvelle méthode en optimisation mathématique qui a fait sa renommée.

C’est avec la sérénité de ceux qui ont trouvé le créneau exact de leur bonheur que Jean-Bernard Lasserre1 nous accueille dans la salle attenante à la bibliothèque du Laboratoire d’analyse et d’architecture des systèmes (Laas – CNRS), à Toulouse. Une fois n’est pas coutume, c’est lui qui entame les questions, porté par la curiosité inhérente au chercheur. Aucun mot n’échappe à l’attention bienveillante de ses yeux bleu-vert. Au moment d’expliquer le cœur de son métier, soucieux de la bonne compréhension de son auditoire, il s’anime soudain, et, tel un peintre dans un élan de création, noircit le tableau blanc de schémas, au fil de ses mots.

Le Graal de l’optimum global

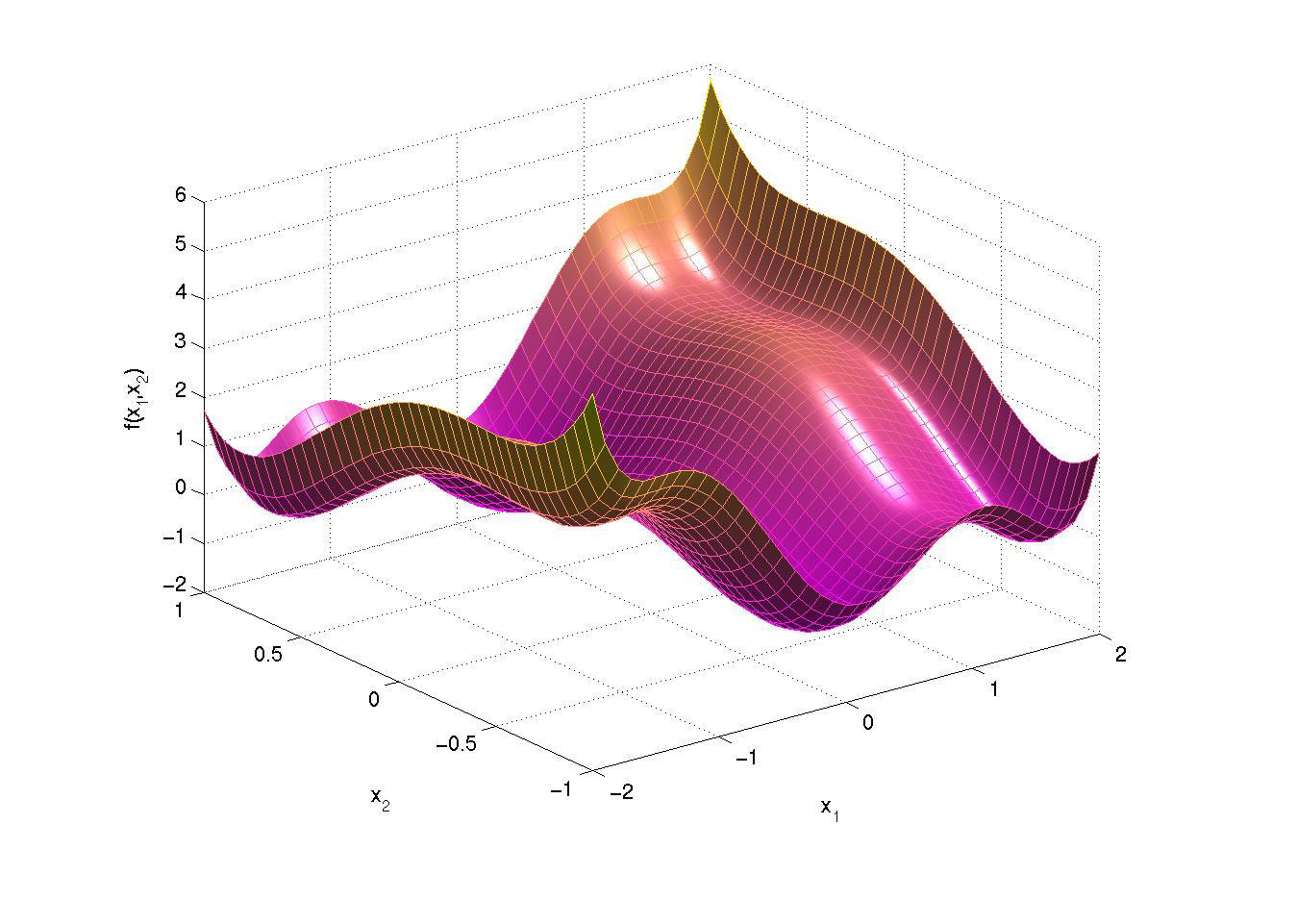
Ainsi, le cœur de son métier, c’est l’optimisation globale, ce champ des mathématiques où l’on cherche à évaluer par le calcul la meilleure option qui soit pour parvenir à un but donné, dans un contexte donné. En termes moins consensuels, il s’agit de minimiser une fonction sur un domaine afin de trouver son optimum global. Comme Jean-Bernard Lasserre aime à le représenter, imaginez que vous êtes en randonnée. « Il est facile, indique-t-il, de trouver le point le plus bas localement, l’optimum local : il vous suffit de descendre. Quand vous ne pouvez plus que monter, vous y êtes. » Par contre, il vous est impossible de savoir empiriquement si vous êtes au point le plus bas de toute la région. Cette altitude la plus basse c’est l’optimum global, le Graal en optimisation.

Polynôme p(x,y) de deux variables "x" et "y", ayant plusieurs minima locaux. Déterminer l'optimum global, soit ici le point plus bas, par le calcul est un exemple des travaux de J.-B. Lasserre.

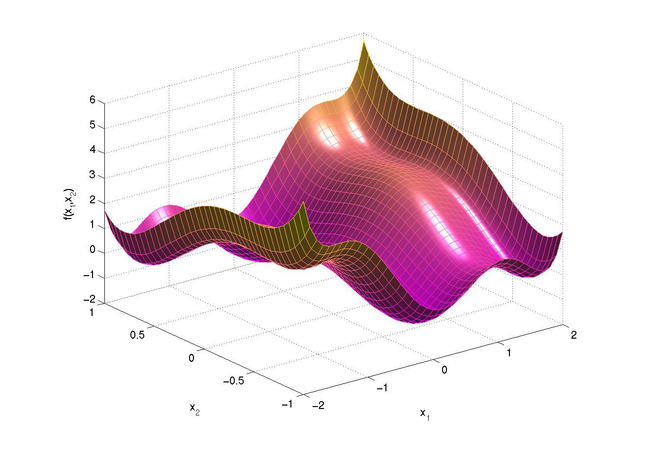
Concrètement, trouver l’optimum global peut par exemple consister, en chimie quantique, à identifier la configuration électronique d’une molécule associée à l’énergie la plus basse possible. Dans les réseaux d’énergie électrique, il peut s’agir de déterminer la meilleure organisation de l’énergie à fournir, correspondant au coût le plus bas pour le fournisseur. Il en va de même en production agricole et industrielle. En fait, quasiment aucun domaine des sciences et de l’ingénierie n’échappe aux problèmes d’optimisation.

Récemment, nous avons montré que notre méthode (hiérarchie de Lasserre) était pertinente et performante dans certains problèmes en statistiques et certaines équations aux dérivées partielles.

Dans certains cas, l’extrême complexité du problème le rend insoluble, que ce soit du fait d’un temps de calcul trop long de l’algorithme mis en place, ou simplement à cause de l’inexistence d’un tel algorithme. C’est ici qu’interviennent les travaux de notre mathématicien, et en particulier la méthode moments-sommes de carrés, ou hiérarchie de Lasserre, à laquelle il a donné naissance en 2000. Cette méthode de calcul permet en effet de résoudre certains problèmes d’optimisation globale auparavant insolubles, ceux dont la description ne requiert que des polynômes et des ensembles semi-algébriques.

Basée sur des résultats de géométrie algébrique réelle des années 1990, celle-ci remplace le problème initial difficile en une suite de problèmes plus simples de taille croissante que l’on sait résoudre efficacement. Comme avec les poupées russes, une fois le premier problème résolu et si un test d’arrêt est négatif, on résout un problème un peu plus gros, et ainsi de suite jusqu’à trouver la solution finale, le fameux optimum global.

Voir autrement pour avancer

Depuis 7-8 ans, entre autres nombreuses collaborations, Jean-Bernard Lasserre accompagne le gestionnaire du réseau de transport d’électricité français (RTE) pour améliorer le passage à plus grande échelle de sa méthodologie déjà utilisée par le groupe. Il étudie également son application en intelligence artificielle, plus précisément en apprentissage profond, pour évaluer et certifier a posteriori la robustesse des calculs en jeu dans les réseaux de neurones.

Améliorer la hiérarchie moments-sommes de carrés et lui trouver de nouvelles applications constituent aujourd’hui l’essence des activités de Jean-Bernard Lasserre. Que ce soit au Laas, en collaboration avec ses collègues de l’Institut de mathématiques de Toulouse2 (IMT) ou dans le cadre de la chaire Polynomial Optimization de l’Institut interdisciplinaire d’intelligence artificielle de Toulouse (Aniti)3 dont il est titulaire. « Récemment, indique-t-il, nous avons montré que notre méthode était pertinente et performante dans certains problèmes en statistiques et certaines équations aux dérivées partielles. J’espère qu’elle pourra être reconnue en tant que nouvel outil complémentaire des techniques plus classiques déjà utilisées dans ces domaines. »

Pylônes haute tension EDF pour le transport d'électricité du réseau RTE. J.-B. Lasserre collabore depuis plusieurs années avec RTE pour optimiser la distribution de l'énergie et les coûts pour le fournisseur.

Cependant, si ce versant de ses recherches est largement dominant ces vingt dernières années, d’autres facettes de l’optimisation ont au cours du temps titillé son intérêt. Au lendemain de sa thèse, c’est par la recherche opérationnelle qu’il a commencé, en gestion et ordonnancement de production, avant de passer une dizaine d’années sur les processus de décision markoviens et chaînes de Markov. À présent, c’est la fonction de Christoffel qui attise sa curiosité. « C’est un autre volet de ma recherche, explique-t-il. Cet outil existe déjà depuis longtemps en théorie de l’approximation. Avec les deux coauteurs de notre livre sur le sujet, nous montrons qu’il peut être utilisé en analyse de données, par exemple pour la détection de données aberrantes. »

Trouver des utilisations novatrices à des outils existants, établir des liens entre des domaines qui semblent a priori différents, c’est un peu le violon d’Ingres de Jean-Bernard Lasserre.

Trouver des utilisations novatrices à des outils existants, établir des liens entre des domaines qui semblent a priori différents, c’est un peu le violon d’Ingres de Jean-Bernard Lasserre. « Si vous les regardez avec des lunettes un peu spéciales, raconte-il, joignant le geste à la parole, vous voyez en fait le même problème. C’est par exemple le cas de la programmation linéaire et entière, de l’intégration et du comptage de points entiers dans un polyèdre. » L’idéal est alors, grâce à ce nouvel angle de vue, de transposer les connaissances d’un domaine plus avancé vers un autre. Même si déjà, saisir l’existence de ces analogies est pour ce passionné une satisfaction en soi.

La recherche en toute liberté

Lorsqu’on lui demande comment il en est arrivé à devenir chercheur en mathématiques appliquées, la réponse a de quoi étonner. Aucune vocation, beaucoup de hasard et de chance, un bon timing. « Mes parents étaient médecins, se souvient-il, ils n’ont jamais cherché à me pousser vers les mathématiques. Je n’ai découvert qu’en terminale l’existence des préparations aux grandes écoles et que les maths me plaisaient bien. » Après une prépa à Toulouse, il embraye sur l’école d’ingénieur Ensimag de Grenoble où les cours d’optimisation l’amènent à choisir son stage de 3^e année dans ce domaine, tout comme le sujet de son doctorat d’ingénieur. C’est le premier déclic – un peu au dernier moment –, il veut faire de la recherche !

J’ai eu des coopérations avec l’Australie, le Mexique... j’adorais découvrir des pays magnifiques tout en travaillant. Et puis le labo est toujours irrigué par des jeunes doctorants, c’est très stimulant.

La deuxième révélation a lieu lors de son postdoctorat à Berkeley, aux États-Unis, juste avant son service militaire en tant qu’appelé scientifique à l’Institut supérieur de l’aéronautique et de l’espace (Isae-Supaéro) à Toulouse. « Là-bas, il y avait encore les traces des sixties, j’adorais ça, s’enthousiasme-t-il. J’allais écouter du rock tous les soirs, l’atmosphère et la liberté étaient incroyables ! Mon parrain, P. Varaiya, était extraordinaire. Et puis le campus de Berkeley, San Francisco… quand vous faites de la recherche dans ces conditions-là, c’est le pied ! C’est là que j’ai su que je voulais entrer au CNRS. Si je n’avais pas pu, je crois que j’aurais été malheureux. »

Et malheureux, il ne l’est pas, c’est même plutôt le contraire. « Le CNRS, c’est la liberté, s’exalte-t-il. Cette espèce de liberté géniale de faire ce qui nous plaît dans notre domaine, de donner libre cours à notre imagination. J’ai eu des coopérations avec l’Australie, le Mexique... j’adorais découvrir des pays magnifiques tout en travaillant. Et puis le labo est toujours irrigué par des jeunes doctorants, c’est très stimulant... ça évite de s’encroûter. Un boulot où vous êtes content d’aller travailler quand vous vous levez le matin, c’est exceptionnel. J’ai eu une chance dans ma vie… ! C’est ce qui fait qu’on se sent redevable d’être sérieux, qu’on espère être utile à la société grâce à laquelle on peut faire ce boulot de rêve. » Si bien que pas un instant, cet amoureux de la liberté ne se voit occuper autrement sa retraite… qu’en continuant la recherche. ♦

Notes

1. Directeur de recherche émérite au CNRS, au Laboratoire d'analyse et d'architecture des systèmes (Laas – CNRS) et à l’Institut de mathématiques de Toulouse (CNRS/Insa Toulouse/Université Tou-louse Paul Sabatier), titulaire de la chaire Polynomial Optimization for Machine Learning and data analysis à l’Institut Aniti.
2. Unité CNRS/Institut national des sciences appliquées de Toulouse/Université Toulouse Paul Sabatier.
3. Artificial and Natural Intelligence Toulouse Institute.

Aller plus loin

0 commentaire