Vous êtes ici
Quand Van Eyck inventait la réalité virtuelle

L’histoire des lignes n’a rien de linéaire, l’importance dans l’art des proportions et de la profondeur a fortement fluctué selon les siècles et les cultures. À la Renaissance, la précision géométrique de la perspective s’est imposée comme un élément essentiel des tableaux et des fresques, mais aussi en architecture ou pour la sculpture. La question a été en particulier traitée par l’historien de l’art Erwin Panofsky, figure tutélaire de la discipline, dans son essai de 1927 La perspective comme forme symbolique.
Des artistes mathématiciens ?
« Au début de la Renaissance italienne, Brunelleschi1 et Alberti2 ont décrit la perspective dans l’art comme une transcription géométrique des lois de l’optique, explique Gilles Simon, maître de conférences à l’université de Lorraine et chercheur au Laboratoire lorrain de recherche en informatique et ses applications (LORIA)3. Ils sont pour cela partis des travaux d’Euclide, en y ajoutant un plan de projection entre l’objet représenté et l’œil du spectateur. »
Une perspective rigoureuse se construit à partir de plusieurs règles mathématiques, comme la présence dans une œuvre d’art de lignes de fuite convergeant en un point unique. Une technique née des maîtres du Quattrocento, et qui semblait inconnue des autres artistes avant que l’influence de la Renaissance italienne ne parvienne jusqu’à eux.

Ainsi, pour Panofsky, le peintre flamand Jan Van Eyck (1390-1441) tentait de s’approcher, de manière empirique, d’une perspective la plus correcte et réaliste possible, mais ignorait les lois géométriques y menant. Van Eyck était pourtant célèbre pour sa rigueur. Il est un des premiers à avoir utilisé la peinture à huile, une technique dont il a élaboré de nouvelles recettes pour obtenir une peinture qui sèche moins vite, et qui lui permettait donc d’apporter plus de détails.
Des algorithmes pour détecter les points de fuite
« En allant admirer le retable de Gand, peint par Van Eyck, j’ai été très impressionné par la perspective sur la fontaine du panneau de l’Adoration de l’Agneau mystique, se souvient Gilles Simon. Je me suis dit qu’il fallait creuser. » Le chercheur est en effet un spécialiste de la détection des lignes et des points de fuite dans les photographies et les vidéos. Ses algorithmes servent par exemple à rectifier les objets déformés par un mauvais angle de vue, ou à guider dans l’espace les systèmes de pilotage autonome.
« Dès que je vais dans un musée, je vérifie malgré moi si la perspective des tableaux semble correcte ou non », s’amuse Gilles Simon. Il a alors adapté certains de ses algorithmes de détection de points de fuite afin de les déployer sur cinq tableaux de Van Eyck, peints entre 1432 et 1439. On retrouve parmi eux son œuvre la plus célèbre, la peinture sur bois des Époux Arnolfini dont la perspective est l’objet d’un bon siècle de débats.

En effet, l’identification de ce qui compte ou non comme une ligne de fuite reste très subjective, chaque historien de l’art peut ajouter ou en exclure certaines, y compris inconsciemment. « J’ai intégré l’incertitude dans les mesures des arêtes, afin d’obtenir une carte probabiliste des points de fuite possibles, détaille Gilles Simon. J’ai également utilisé une ancienne méthode informatique pour faire ressortir les pics de probabilités les plus significatifs. »
Une « machine à perspective »
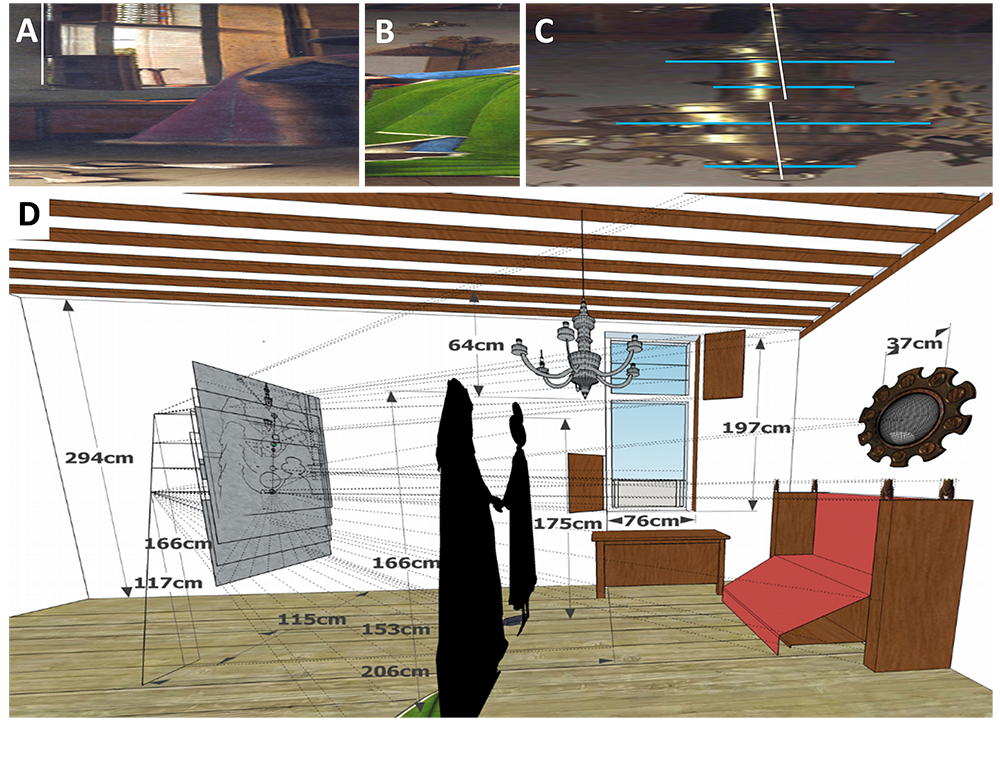
Il a ainsi montré que les Époux Arnolfini est composé de quatre bandes horizontales, possédant chacune un point centrique régulièrement espacé le long d’un axe incliné parcourant le tableau dans sa hauteur. À l’intérieur de ces bandes, la perspective obéit parfaitement aux lois géométriques dont on pensait que seuls quelques maîtres italiens avaient alors le secret.
Si cette organisation n’a pas été retrouvée dans l’Adoration de l’Agneau mystique, les cinq tableaux étudiés partagent tous un schéma en arête de poisson qui n’avait jamais été identifié avant les travaux de Gilles Simon. Ces derniers ont été rendus publics lors de la conférence internationale ACM in Computer Graphics and Interactive Techniques, qui s’est déroulée du 9 au 13 août 2021.
Gilles Simon y présente également une reconstitution en 3D de la perspective multiple du tableau, et explique comment Van Eyck s’y est pris. Le peintre aurait ainsi utilisé une véritable « machine à perspective » composée de quatre œilletons équidistants, un pour chaque bande, disposés verticalement.
« Il commence par dessiner une première bande, tout en haut ou tout en bas, à travers un œilleton, détaille Gilles Simon. Mais à cause du phénomène de parallaxe, l’image se décale lorsqu’il passe au second œilleton. Il compense cela en suivant un axe du décor, puis fait de même avec les bandes restantes. La géométrie 3D empêche cependant un alignement parfait. On aperçoit ainsi encore un peu de décalage dans le tableau final, en particulier au niveau du chandelier dont l’aspect s’explique par le fait qu’il se tienne à cheval sur deux bandes. »
Un précurseur de la réalité virtuelle
Si Brunelleschi employait autour de 1420 un panneau de bois percé d’un œilleton, Van Eyck n’en reste pas moins un des pionniers de l’utilisation de systèmes optiques pour rendre la perspective et tenir compte de notre vision stéréoscopique. Cette approche peut être considérée comme les prémices de la réalité virtuelle, et sera simplifiée soixante-dix ans plus tard par Léonard de Vinci.
Fort de sa découverte, Gilles Simon applique à présent sa méthode à d’autres œuvres, au-delà de Van Eyck, et s’attend à de nouvelles surprises quant à l’usage de la perspective. Il souligne également que sa technique pourrait aider à authentifier certains tableaux.
Les algorithmes de Gilles Simon restent cependant difficiles d’accès pour qui n’est pas spécialiste, mais il souhaite concevoir une interface qui les rendra utilisables par les historiens de l’art. « Ils sont encore peu nombreux à s’intéresser à l’informatique, déplore Gilles Simon, mais j’espère que des travaux comme les miens vont les pousser à employer nos outils. Cela fait une bonne trentaine d’années que nous avons développé des solutions qui pourraient les aider à résoudre leurs problèmes géométriques. » ♦
- 1. Filippo Brunelleschi (1377-1446) est principalement connu comme l’architecte du dôme de la cathédrale Santa Maria del Fiore à Florence.
- 2. Leon Battista Alberti (1404-1472), lui aussi architecte, a notamment conçu les façades du palais Rucellai et de Santa Maria Novella, là encore à Florence.
- 3. CNRS/Université de Lorraine/INRIA.
Voir aussi
Auteur
Diplômé de l’École supérieure de journalisme de Lille, Martin Koppe a notamment travaillé pour les Dossiers d’archéologie, Science et Vie Junior et La Recherche, ainsi que pour le site Maxisciences.com. Il est également diplômé en histoire de l’art, en archéométrie et en épistémologie.