Vous êtes ici
La cryptographie face à la menace quantique
Comment le mathématicien que vous êtes en est-il venu à concevoir des codes secrets ?
Benjamin Wesolowski1. D’aussi loin que je me souvienne, j’ai toujours aimé les mathématiques. J’ai donc suivi cette passion, qui m’a conduit à intégrer l’École polytechnique fédérale de Lausanne, où j’ai passé ma licence, mon master, puis mon doctorat. C’est là que j’ai vraiment découvert la cryptologie, une discipline qui a tout de suite séduit l’amoureux des mathématiques que j’étais (et que je suis toujours) ! Mais cette histoire a peut-être commencé bien avant : enfant, j’adorais les jeux d’espion dans les magazines qui consistaient à déchiffrer un texte codé.
Un parcours qui vous a mené jusqu’à devenir lauréat de l’ERC Starting Grant 2023. De quoi s’agit-il ?
B. W. L’ERC Starting Grant est une bourse attribuée par le Conseil européen de la recherche, finançant les travaux de jeunes chercheurs. Dans mon cas, le projet financé vise à solidifier les bases de la cryptographie fondée sur les réseaux euclidiens et les isogénies. Mon but est ainsi d’utiliser des théories mathématiques déjà connues, mais jusqu’ici peu employées dans le domaine de la cryptographie. Or, ces outils peuvent apporter une nouvelle vision à la discipline et contribuer au développement de nouveaux fondements rigoureux, notamment pour estimer la complexité des problèmes.
La cryptographie a connu une avancée majeure dans les années 1970, lorsque les cryptographes ont commencé à puiser dans des théories mathématiques jusqu’alors inexploitées, comme la théorie des nombres. Cette avancée majeure, c’est la cryptographie à clé publique. La discipline est aujourd’hui confrontée à de nouveaux défis, posés notamment par les ordinateurs quantiques. Les problèmes deviennent de plus en plus complexes, et l’exploration mathématique joue un rôle de plus en plus important.
Quelle est la différence entre cryptographie à clé publique et cryptographie à clé secrète ?
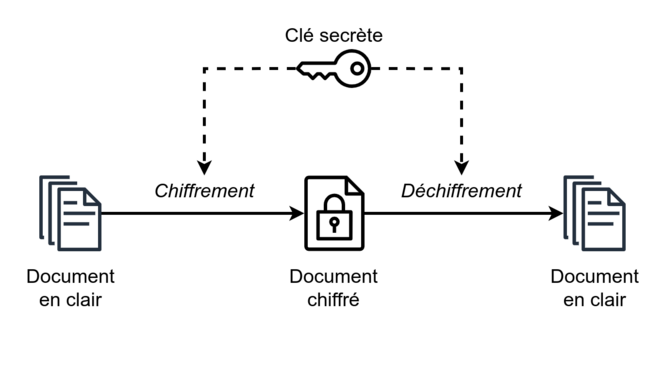
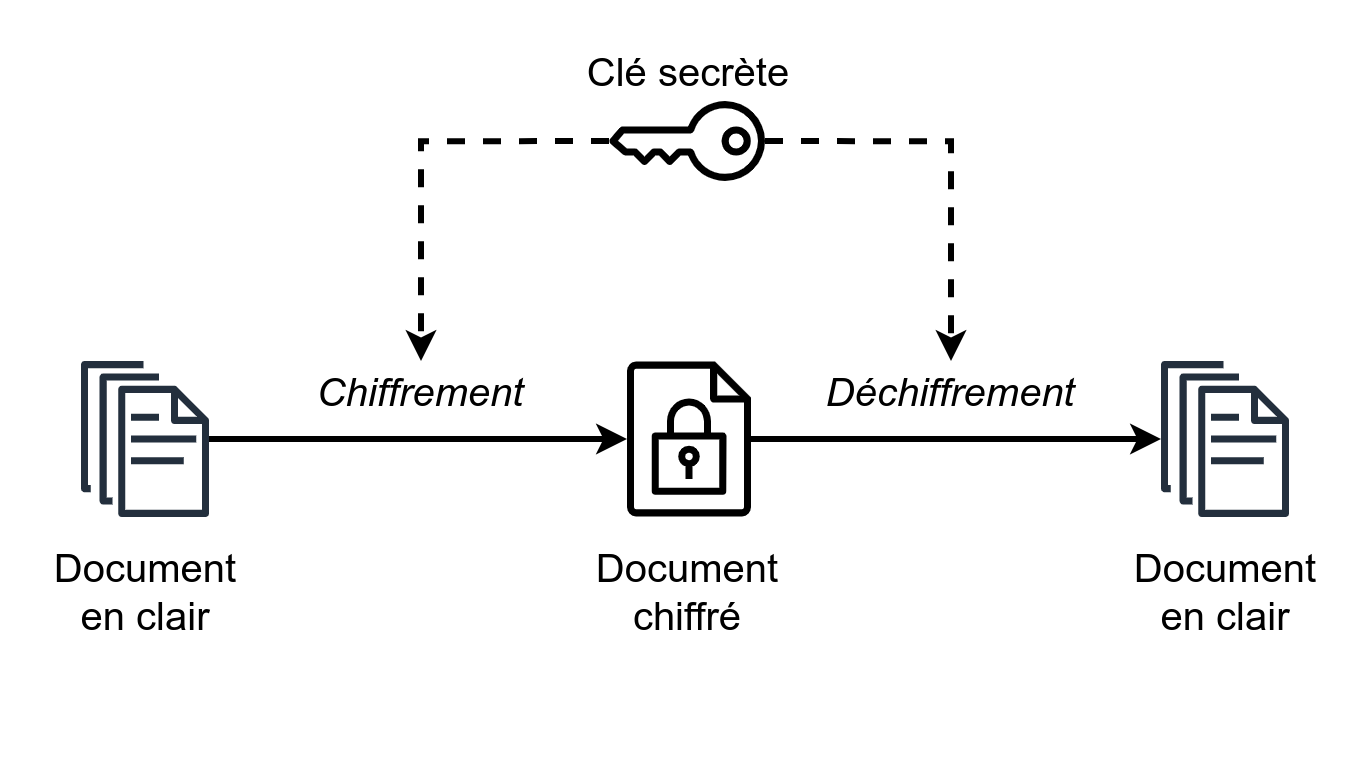
B. W. La cryptographie à clé secrète est la méthode la plus ancienne. L’idée est simple : deux interlocuteurs veulent communiquer en secret sur un canal non sécurisé (tous leurs messages peuvent être interceptés). Ils se mettent d’accord sur un procédé de chiffrement, permettant de transformer un message en un texte inintelligible, envoyé sur le canal, puis déchiffré par le destinataire. Pour que seul le destinataire puisse déchiffrer le message, les interlocuteurs se sont au préalable mis d’accord sur un ingrédient secret permettant le chiffrement et le déchiffrement : la clé secrète. Un espion, sans la clé secrète, ne peut pas lire le texte intercepté.
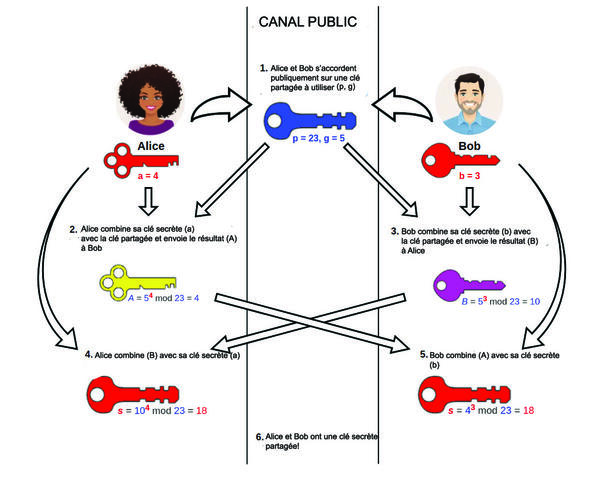
La cryptographie à clé publique répond à la question suivante : comment les interlocuteurs peuvent-ils choisir une telle clé secrète, sans avoir à se rencontrer physiquement ? Toutes leurs communications peuvent être interceptées et ils n’ont pas encore choisi de clé secrète commune, donc comment pourraient-ils se mettre d’accord sur un secret (la clé elle-même) ? C’est un problème que l’on a longtemps pensé insoluble, jusqu’à l’invention de la cryptographie à clé publique.
Comment fonctionne-t-elle ? Pourquoi est-elle aujourd’hui si employée pour la sécurité de nos communications ?
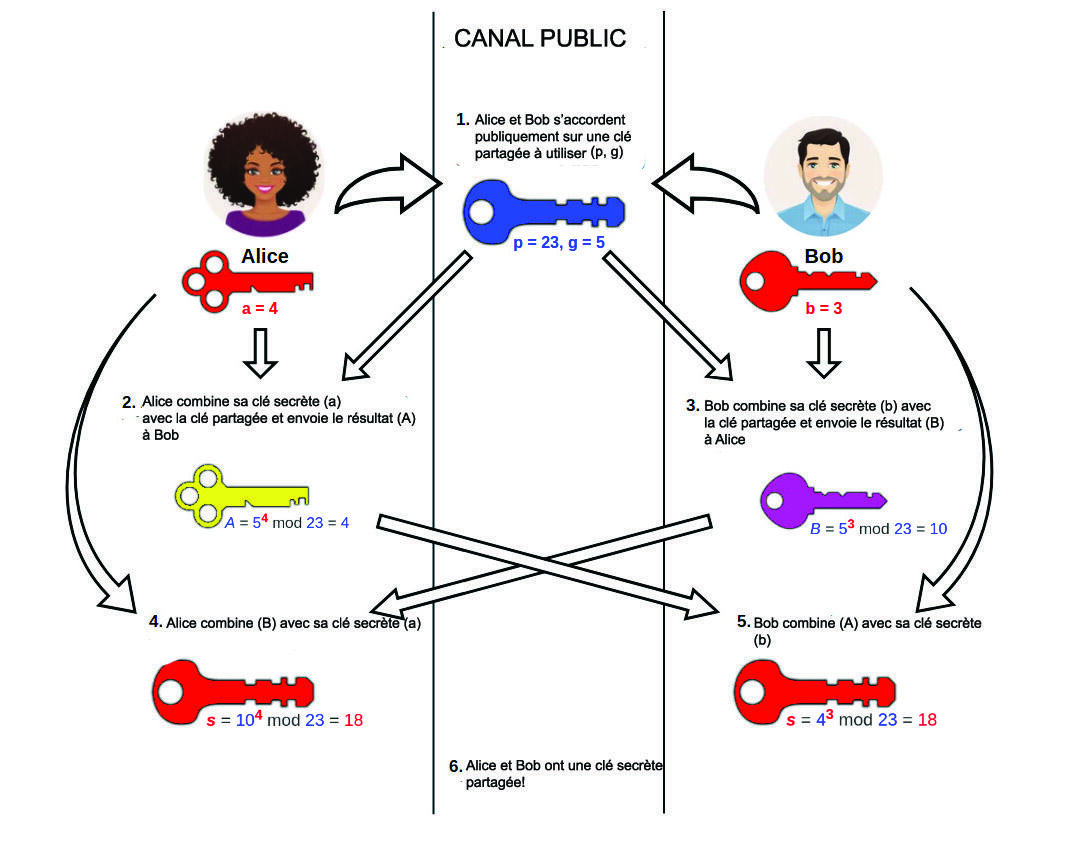
B. W. Le protocole de Diffie-Hellman, qui a été le premier en la matière et qui est encore très utilisé de nos jours, a un fonctionnement assez simple. Les interlocuteurs commencent par se mettre d’accord sur un « nombre » n, qui n’est pas secret. Le premier choisit en secret un nombre entier x, et envoie nx. Le second choisit également en secret un nombre entier y, et envoie ny. Chacun des interlocuteurs est en mesure de calculer nxy. En effet, le premier connait x (son secret) et ny (qui lui a été envoyé) et peut donc calculer (ny)x. De manière similaire, le second peut calculer (nx)y. Un espion aura pu intercepter n, nx et ny, mais le « nombre » nxy n’a jamais transité sur le canal non sécurisé : c’est un secret partagé par les interlocuteurs, qui peut désormais leur servir de clé secrète.
En réalité, voyant nx, un espion pourrait tenter de retrouver x : c’est ce qu’on appelle un logarithme. S’il y parvient, il pourra calculer (ny)x, et tout s’écroule. Calculer des logarithmes pour des nombres usuels est facile. En revanche, n peut être choisi parmi d’autres types de « nombres » où ce problème est bien plus dur. C’est ce qu’on appelle le problème du logarithme discret.
Plusieurs méthodes ont toutefois été mises au point pour le résoudre, de manière plus efficace que la simple recherche exhaustive. Cependant, elles nécessitent tout de même une énorme puissance de calcul lorsque les nombres impliqués sont très élevés. Cela signifie qu’avec des paramètres suffisamment grands, même faire tourner tous les ordinateurs du monde, pendant plusieurs milliards d’années, ne suffit pas pour résoudre le problème. C’est pourquoi on considère le problème du logarithme discret comme difficile et le protocole de Diffie-Hellman comme sûr pour protéger nos communications.
Pour des ordinateurs classiques, d’accord. Mais qu’en serait-il avec un ordinateur quantique ?
B. W. La donne serait bien différente ! En supposant qu’un individu ait accès à un ordinateur quantique suffisamment stable, il pourrait alors résoudre le problème du logarithme discret de façon efficace.
Et donc casser de nombreux protocoles de cryptographie. Néanmoins, cela ne veut pas dire qu’un ordinateur quantique consiste juste en une sorte de super ordinateur classique, beaucoup plus puissant. Simplement, il fonctionne différemment : à la place des bits classiques, il s’appuie sur des bits quantiques, qui permettent d’encoder en superposition de nombreux états différents. Cette propriété offre un avantage aux ordinateurs quantiques pour résoudre certains problèmes – un avantage parfois considérable, mais encore une fois, seulement pour certains problèmes. Et le problème du logarithme discret figure justement parmi ceux pour lesquels l’ordinateur quantique serait bien plus efficace !
Faut-il donc s’inquiéter pour la sécurité de nos communications ?
B. W. S’inquiéter aujourd’hui, non. Car l’ordinateur quantique relève pour l’heure de la théorie. Les prototypes existants ne sont pas capables de casser les méthodes actuelles de cryptographie.
Mais qu’arrivera-t-il si on parvient à créer un ordinateur quantique suffisamment gros et stable ?
B. W. Il vaudrait mieux ne pas attendre que la menace apparaisse pour se poser la question ! En effet, s’il faut changer tous nos standards de communication, cela prendra plusieurs années. De plus, on peut aisément imaginer que des individus ou agences de renseignement prennent bien soin d’enregistrer les échanges chiffrés actuels. Ils sont peut-être incapables de les lire aujourd’hui, mais cela deviendra une mine d’informations le jour où ils auront accès à un ordinateur quantique. C’est une attaque dite « récolte maintenant, déchiffre plus tard ». Cela a déjà eu lieu par le passé. Dans le cadre du projet Venona, les services de renseignement américains avaient intercepté des communications soviétiques chiffrées émises pendant la Seconde Guerre mondiale. Le code ayant été craqué en 1946, ils sont ensuite parvenus à déchiffrer progressivement les messages, découvrant notamment l’étendue de l’espionnage atomique au profit de l’URSS durant le projet Manhattan.
Alors comment faire pour rendre la cryptographie robuste aux ordinateurs quantiques ?
B. W. En remplaçant les problèmes vulnérables, tels que le problème du logarithme discret, par des problèmes plus difficiles, résistants aux algorithmes quantiques. Pour cela, il faut identifier des problèmes candidats et tester leur difficulté. C’est là que la cryptologie algorithmique joue un rôle fondamental : il s’agit de mettre au point les meilleurs algorithmes permettant de résoudre ces problèmes, pour tester leurs limites. Et en étudiant ces techniques, nous pouvons adapter les méthodes de cryptographie, afin de les rendre plus résistantes aux potentielles attaques. Cette approche algorithmique s’applique de manière générale, pas seulement dans une perspective post-quantique. Durant des décennies, la cryptologie algorithmique a persécuté les problèmes classiques comme le logarithme discret. Aujourd’hui, l’effort collectif est largement redirigé vers les problèmes post-quantiques.
Quels autres problèmes, par exemple ?
B. W. Il y a plusieurs candidats, dont certains autour des réseaux euclidiens. Un réseau euclidien est un arrangement régulier de points dans l’espace, comme les points d’intersection d’une grille. Un des problèmes étudiés est le suivant : dans un maillage donné, quels sont les deux points les plus proches possibles ? Pour une grille carrée, en 2D, la réponse est facile à trouver. Mais si la grille n’est pas si simple, et dans une dimension 100, 200 ou 500, alors la tâche est beaucoup plus difficile. Même pour un ordinateur quantique – c’est du moins ce que l’on espère, et nous continuons de mettre cette hypothèse à l’épreuve.
Un autre candidat repose sur les courbes elliptiques et les isogénies. Il s’agit de concepts mathématiques assez abstraits, donc plus difficiles à expliquer en quelques mots. Pour faire simple, dans certains cas, deux courbes elliptiques peuvent être reliées par une « isogénie » – une formule permettant de passer de l’une à l’autre. Le problème, que l’on suppose difficile, est alors le suivant : pour deux courbes données, peut-on trouver l’isogénie qui les relie ?
Ces deux problèmes sont ceux auxquels je m’intéresse principalement à l’heure actuelle.♦
A lire sur notre site
Vers une cryptographie post-quantique
- 1. Unité de mathématiques pures et appliquées (CNRS/ENS Lyon).
Voir aussi
