Vous êtes ici
Quand les maths se mêlent de sport
Temps de lecture : 5 minutes
Aux prochains Jeux olympiques de Rio, les athlètes australiens et néo-zélandais ne viendront pas accompagnés de leurs seuls entraîneurs et médecins : ils auront dans leurs équipes techniques des… mathématiciens et des physiciens. Surprenant ? Pas tant que ça. « Les Anglo-Saxons ont compris depuis longtemps l’avantage que le sport de haut niveau peut tirer des mathématiques, et les chercheurs de ces pays conçoivent pour leurs champions des logiciels d’aide à la performance quasi sur mesure », raconte Amandine Aftalion, directrice de recherche au Laboratoire de mathématiques de Versailles1 et instigatrice de la rencontre « Maths et sport » qui s'est tenue le 15 mars à l’Institut Henri Poincaré2. L’amélioration de la performance n’est pas le seul sujet qui intéresse les chercheurs anglo-saxons : ainsi, des mathématiciens britanniques ont mis au point un outil capable de prédire le nombre de médailles qui seront décrochées dans chaque discipline. S’il n’est pas capable de prédire l’irruption du prochain Usain Bolt, le logiciel donnerait une bonne estimation des moissons de récompenses à venir…
Courir la course optimale
Plus naturellement portés à l’abstraction que leurs collègues anglo-saxons, les mathématiciens français commencent tout juste à s’intéresser aux terrains de sport… Mais les travaux déjà publiés donnent une idée du potentiel de ce mariage. Amandine Aftalion s’est ainsi penchée sur les performances des coureurs à pied et a développé un modèle permettant aux athlètes de courir la course optimale, en fonction de la distance à parcourir – du 80 mètres au 1 500 mètres – et de quatre paramètres clés : la capacité pulmonaire, les apports énergétiques, la force maximale de propulsion mais aussi les frottements du corps. « On vient d’affiner le modèle général pour pouvoir l’adapter aux caractéristiques de chaque individu », précise la chercheuse3. Reste à intégrer un paramètre de taille, encore non pris en compte par le modèle : le facteur psychologique – en un mot, la motivation !
domaine où peu
de scientifiques
s’aventurent. C’est
encore un espace
vierge où il y a
tout à trouver.
Mais les maths ne servent pas qu’à améliorer les performances sportives. Observer les phénomènes physiques à l’œuvre sur les terrains de sport permet aussi de découvrir de nouvelles lois à formaliser. « Le sport est un domaine qui n’est pas “politiquement correct” pour la recherche et où peu de scientifiques s’aventurent. C’est encore un espace vierge où il y a tout à trouver », s’enthousiasme Christophe Clanet. Ce physicien du Laboratoire d’hydrodynamique4 est spécialiste des trajectoires des particules dans les fluides, quels qu’ils soient : gouttes, bulles, mais aussi balles et ballons au-dessus des terrains de sport !
Un coup franc inspirant
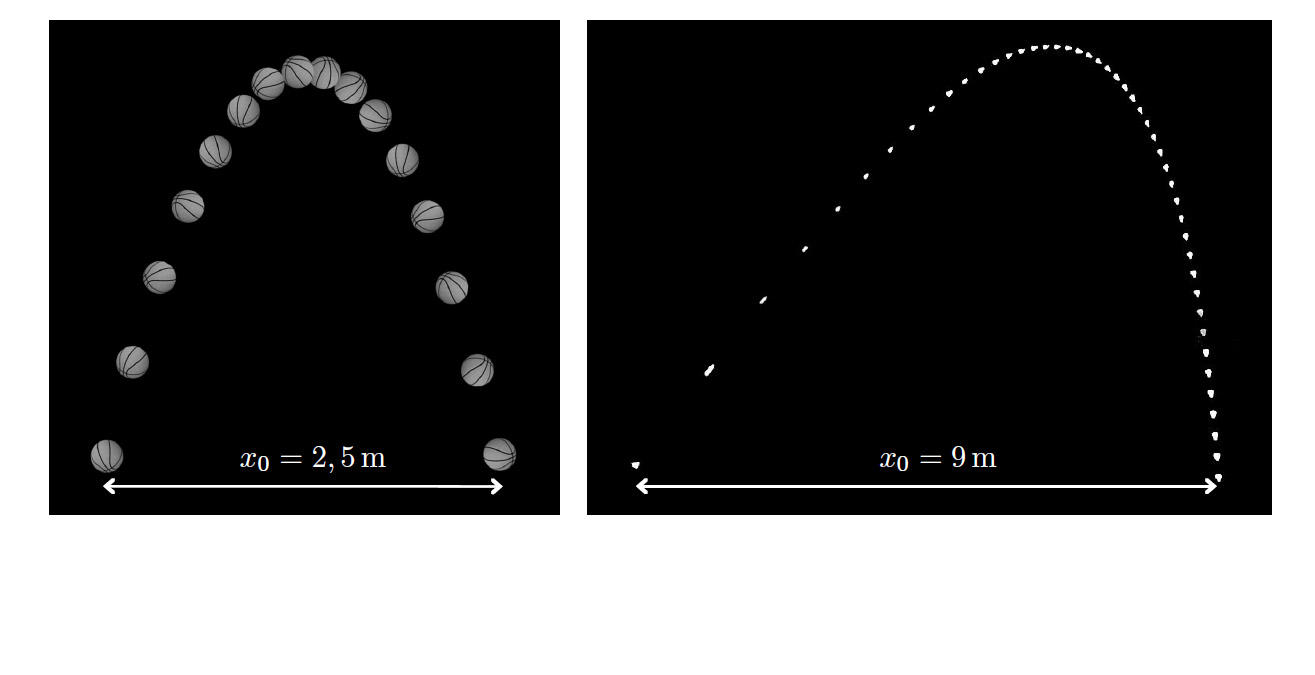
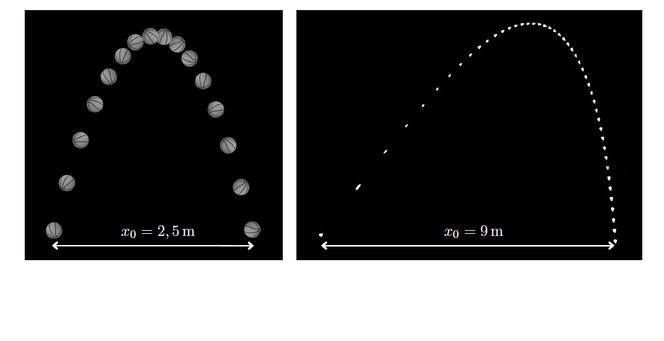
« C’est en discutant avec les jeunes chercheurs de mon équipe du célèbre coup franc de Roberto Carlos, au Tournoi de France de 1997, qu’on a décidé de creuser la question », raconte le scientifique. À tort, on pense que les balles suivent des trajectoires paraboliques. En étudiant les trajectoires de ces projectiles dans différents sports, les chercheurs se sont rendu compte que c’était le cas de deux disciplines uniquement : le basket et le handball. Toutes les autres balles, du tennis de table en passant par le football ou le badminton, génèrent des trajectoires triangulaires dites Tartaglia, du nom d’un mathématicien italien du XVIe siècle5. « Deux facteurs sont à prendre en compte, poursuit Christophe Clanet. La vitesse maximale à laquelle la balle peut être lancée et sa vitesse de lévitation – autrement dit, la vitesse du flux d’air qu’il faudrait générer pour l’empêcher de toucher le sol. » Lorsque la vitesse de lévitation est supérieure à la vitesse de lancer, la trajectoire est parabolique. C’est le cas au basket, avec une vitesse de lévitation de 31 m/s et une vitesse de lancer de 16 m/s. À l’inverse, lorsque la vitesse de lévitation est inférieure à la vitesse de lancer, alors la trajectoire prend la forme d’une Tartaglia. C’est le cas au football ou encore au badminton.
Autre loi mise au jour par les chercheurs : la distance maximale que la balle peut couvrir avec un lancer dépend elle aussi de ces deux paramètres. « Au-delà, il existe un mur invisible que la balle ne pourra pas franchir, quelle que soit la force avec laquelle on l’engage sur le terrain », précise Christophe Clanet. Une loi physique qui trouve des applications bien au-delà du domaine sportif, puisque le travail des chercheurs a notamment servi à discuter de l’amélioration de la portée des lances à incendie utilisées par les pompiers (où l’on observe aussi des Tartaglia). Ou comment le tir d’un footballeur brésilien permet de mieux armer les combattants du feu.
- 1. Unité CNRS/Univ. Versailles Saint-Quentin.
- 2. La journée « Maths et sport » est organisée par la Smai (Société de mathématiques appliquées et industrielles), avec le soutien de l’Amies (Agence pour les mathématiques en interaction avec l’entreprise et la société). Pour en savoir plus : http://mathsetsport.sciencesconf.org
- 3. « How to identify the physiological parameters and run the optimal race », A. Aftalion et al., Mathematics in action, janvier 2016, vol. 7 (1) : 1-10.
- 4. Unité CNRS/École polytechnique.
- 5. Niccolò Fontana, dit Tartaglia (« Le Bègue »), s’est notamment illustré par ses travaux sur la balistique des boulets de canon.
Voir aussi
Auteur
Journaliste scientifique, Laure Cailloce est rédactrice en chef adjointe de CNRS Le Journal et de la revue Carnets de science.