Vous êtes ici
Des graphes pour planifier le déconfinement ?
Vous proposez d’appliquer les outils issus de la théorie des graphes pour étudier la propagation du Covid-19. Quels sont l’origine et l’objectif de ce projet ?
Claire Mathieu1 : Dans le cadre de la lutte contre le coronavirus, la direction du CNRS invite l’ensemble de ses personnels à faire des propositions de travaux de recherche potentiellement utiles. En discutant il y a quelques jours avec mes collègues Laurent Viennot et Vincent Cohen-Addad, nous nous sommes dit que nos travaux sur les graphes pourraient peut-être avoir un intérêt pour étudier la propagation du virus au sein de petites communautés et ainsi éclairer la mise en place de stratégies de déconfinement.
Qu’est-ce qu’un graphe et quel est le lien avec la propagation des épidémies ?
C. M. : Un graphe est un réseau de points, appelés nœuds, reliés par des liens. Dans le cadre d’une épidémie, chaque nœud représente une personne se trouvant à un stade infectieux donné (saine, infectée ou guérie) et chaque lien entre deux nœuds matérialise une interaction sociale entre deux individus. Le tout fournit une sorte de carte de l’ensemble des contacts sociaux au sein d’un groupe.
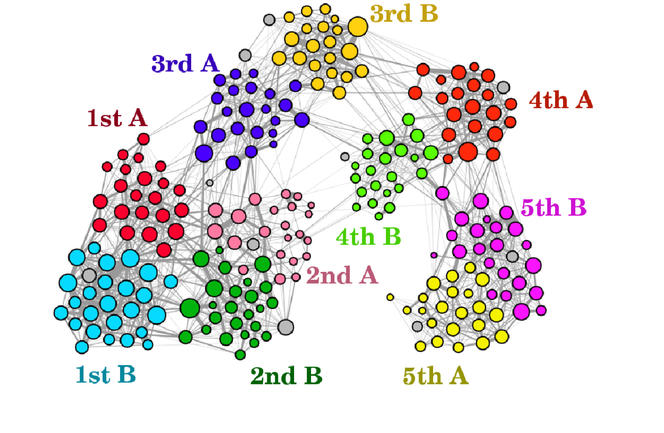

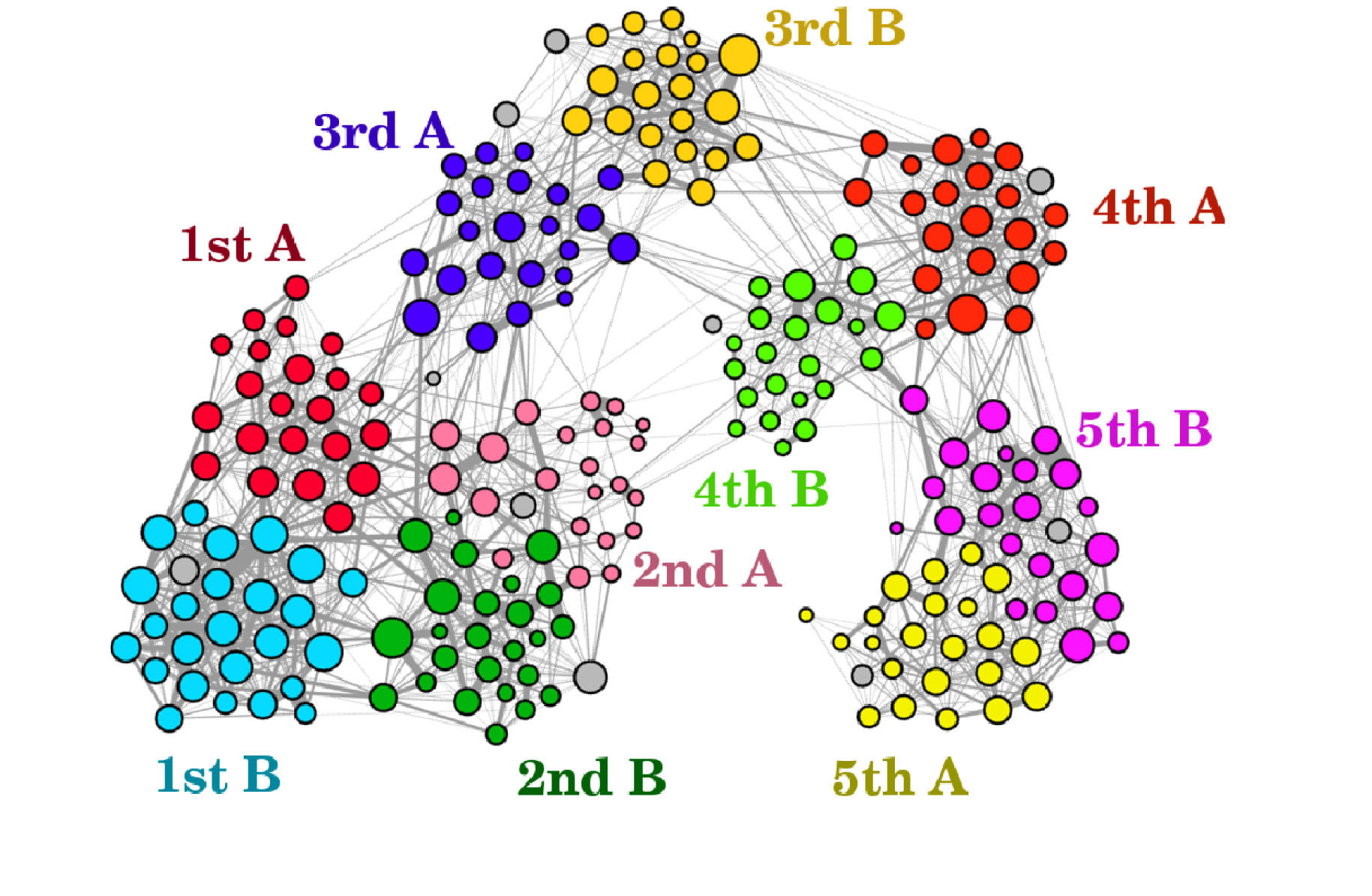
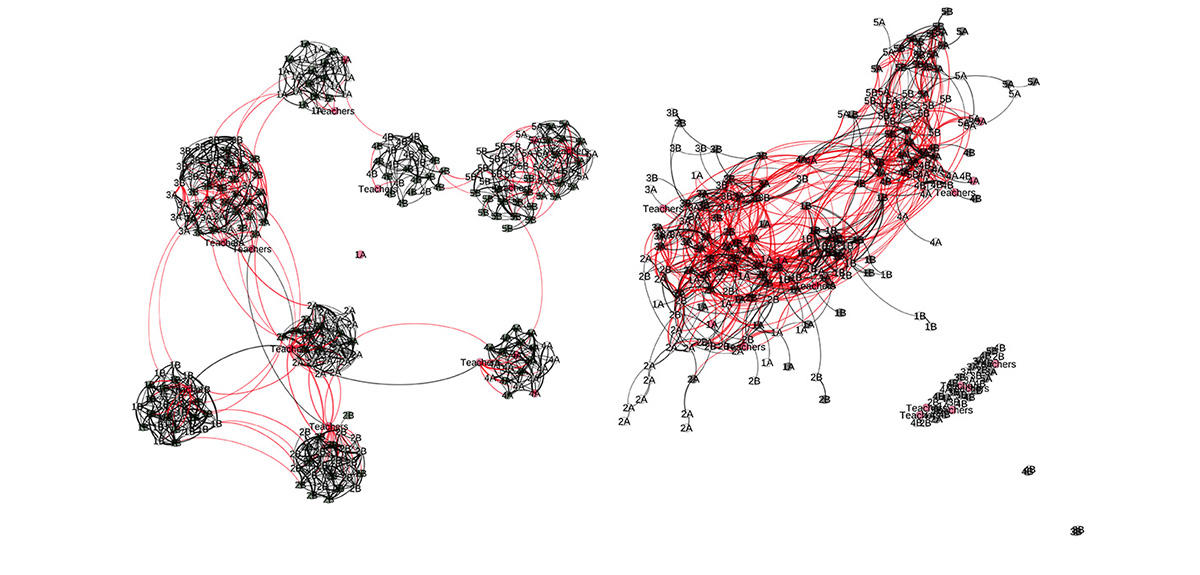
Par exemple, si je considère le graphe des interactions sociales de mon quartier en cette période de confinement, il apparaîtra que je suis reliée à très peu de personnes, essentiellement ma famille d’une part et les commerçants chez qui je m’approvisionne d’autre part, alors que mon boulanger, lui, entretient des liens avec un nombre très important d’habitants de par son activité. À partir de ce réseau, on se donne ensuite une probabilité pour la transmission du virus lors d’une interaction entre deux personnes appartenant au réseau, et de là on peut étudier la façon dont l’infection se propage au sein de la population.
Par des modélisations similaires, les chercheurs en informatique ont par le passé étudié la façon de propager au mieux une information au sein d’un groupe, d’où il ressort, pour le dire vite, l’importance des individus très connectés, ainsi que de ceux qui appartiennent à plusieurs communautés simultanément. Pour propager une information, il faut donc les privilégier. À l’inverse, ce sont eux qu’il faudrait isoler en premier pour contenir une épidémie.
Que peut apporter ce type de modélisation par rapport à celles déjà utilisées par les épidémiologistes ?
C. M. : D’une manière générale, la modélisation d’un phénomène complexe requiert différents modèles adaptés aux différentes échelles spatiotemporelles à considérer. Dans le cas des modèles climatiques par exemple, si on peut résoudre numériquement les équations de la physique qui décrivent un phénomène à très petite échelle, on doit utiliser des représentations statistiques aux grandes échelles, et encore d’autres modèles aux échelles intermédiaires. Concernant la propagation d’une épidémie, notre proposition pourrait s’appliquer à l’échelle de la granularité la plus fine, pour des communautés réduites dont on prendrait en compte tous les liens.
Concrètement, qu’allez-vous faire ?
C. M. : Des collègues physiciens, dans le cadre d’un projet intitulé Socio-patterns, ont mis à la disposition du public des données collectées en 2011 dans une école primaire, qui contiennent la totalité des interactions de l’ensemble des élèves et enseignants pendant deux jours : qui croise qui, quand, où, combien de temps ? Ainsi, le graphe dynamique correspondant comprend environ 250 nœuds et plusieurs centaines de milliers de liens, et on peut analyser ses propriétés de propagation dans le but d’étudier différentes stratégies pour la réouverture des écoles. Faut-il ouvrir la moitié du temps ? Séparer les élèves en plusieurs groupes ? Si oui, quelle serait leur taille optimale ? Les enfants doivent-ils ou pas déjeuner dans leur classe ? N’est-il pas préférable de déplacer les professeurs de collège et de lycée de classe en classe plutôt que les élèves ? Une analyse quantitative rigoureuse peut aider à répondre à ces questions.
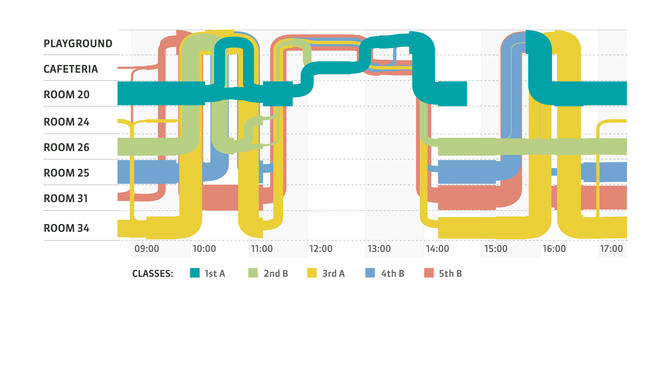

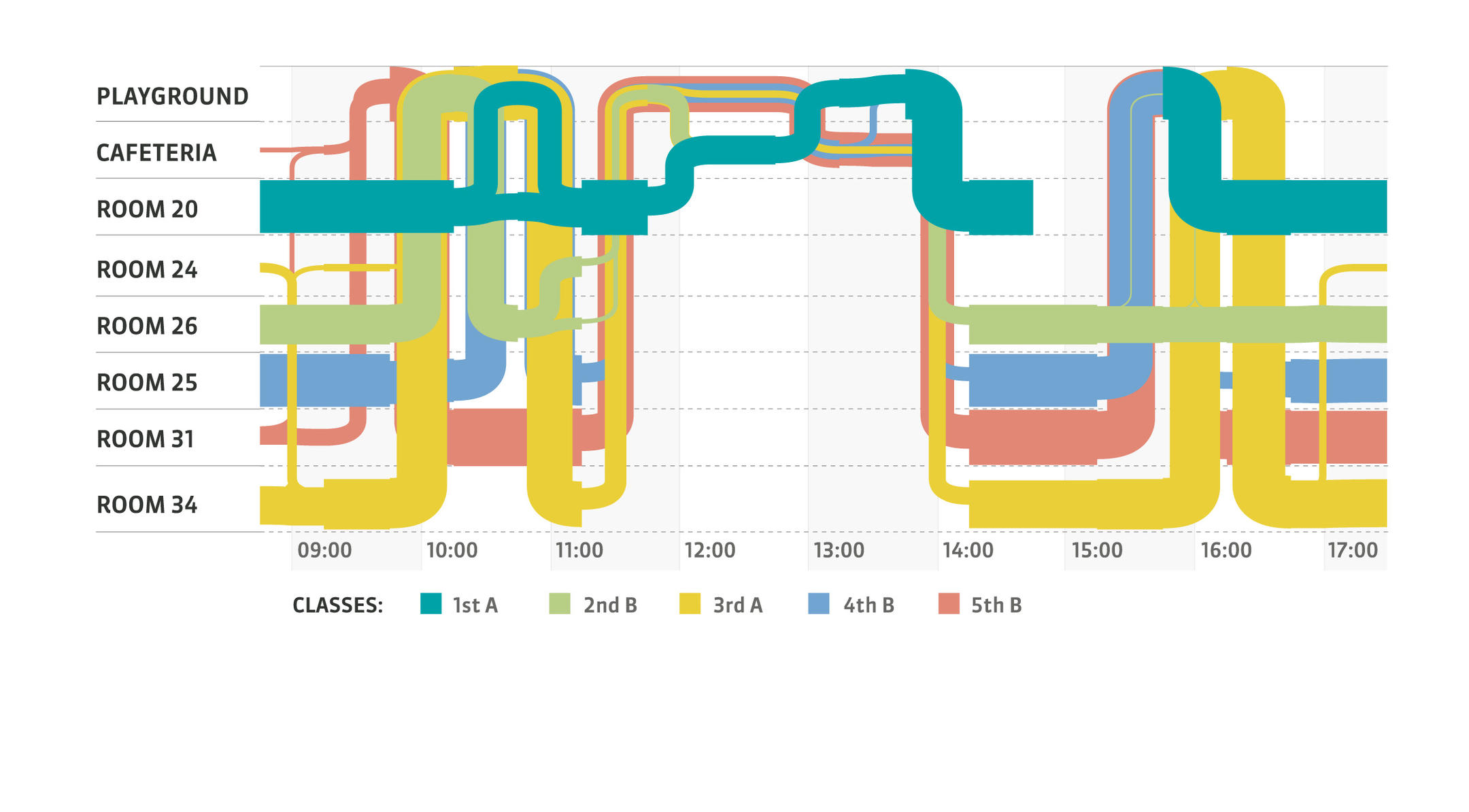
Ensuite, nous envisageons de modéliser théoriquement des réseaux d’interactions représentatifs de différentes situations à partir desquelles conduire des analyses similaires. Il serait intéressant de modéliser les liens typiques au sein d’une famille, d’un établissement scolaire et d’une entreprise, puis de lier entre eux les différents graphes correspondants afin de comprendre par quels « chemins » précis passe une épidémie. Nous pourrions peut-être alors aider à éclairer la réflexion sur les différents scénarios de déconfinement à l’étude à l’échelle d’une ville ou d’un quartier, concrètement en indiquant quels sont les liens les plus pertinents à maintenir inactifs.
Le 13 avril, le président de la République a annoncé la réouverture des établissements scolaires le 11 mai. À ce stade de vos travaux, que pouvez-vous en dire ?
C. M. : Qu’il est pour nous beaucoup trop tôt pour affirmer quoi que ce soit ! Il faut garder à l’esprit qu’en temps normal, un travail de recherche nécessite au moins six mois avant que l’on puisse éventuellement en tirer des conclusions préliminaires. Or ici, nous avons émis une proposition il y a une quinzaine de jours et avons commencé à travailler peu après. Cela étant, on peut imaginer que les chercheurs puissent jouer un rôle de conseil auprès des recteurs ou des chefs d’établissement pour aider à réorganiser les écoles, soit à partir du 11 mai, soit après l’été.
Par ailleurs, supposons que nous revenions d’ici quelques semaines à une situation équivalente au premier stade épidémiologique (sauf en ce qui concerne les personnes qui seraient immunisées). Il s’agirait alors, dès qu’une nouvelle personne malade se présente, d’une part de l’isoler, d’autre part de tester ses contacts afin de les isoler le cas échéant, avant même qu’ils ne soient eux-mêmes contagieux. On peut imaginer que notre approche puisse aider à déterminer les priorités en matière de placement à l’isolement de ces personnes. De fait, si certains liens à couper semblent évidents, d’autres, plus subtils, pourraient n’être mis en évidence que par une analyse mathématique rigoureuse.
Les résultats de vos travaux sont-ils susceptibles de servir de données d’entrée pour « nourrir » des modèles épidémiologiques à plus grande échelle, rendant ainsi leurs prédictions plus précises ?
C. M. : Là encore, il est bien trop tôt pour répondre, mais c’est une question naturelle. Plus généralement, je voudrais insister sur le fait que dans la période d’incertitude où nous nous trouvons, toutes les questions ou remarques, d’où qu’elles viennent, sont susceptibles de nourrir la réflexion. Dans le cas des écoles, les graphes apporteront peut-être des éléments de réponse, mais il serait également très intéressant d’intégrer à la réflexion des directeurs d’école, des professeurs et des parents. Par exemple, admettons que nos modèles suggèrent que d’un strict point de vue épidémiologique, pour couper les liens qui présentent la plus forte probabilité de transmettre le virus, il soit préférable de séparer les bons copains. Est-ce réellement souhaitable du point de vue de l’organisation d’un établissement scolaire ? Ce n’est pas à moi de répondre. Mais ce que je sais, c’est qu’au sein du réseau formé par la société, à plus forte raison s’agissant de questions complexes sur lesquelles il convient d’apporter des réponses rapidement, la circulation des informations et des expériences susceptibles de nourrir la discussion doit se faire de la façon la plus horizontale possible ! ♦
À lire sur le site du journal
Comment mieux prédire les épidémies
- 1. Informaticienne et mathématicienne, directrice de recherche au CNRS à l'Institut de recherche en informatique fondamentale (CNRS/Université de Paris/Inria). Claire Mathieu est lauréate de la médaille d'argent du CNRS 2019.
Voir aussi
Auteur
Né en 1974, Mathieu Grousson est journaliste scientifique. Diplômé de l’École supérieure de journalisme de Lille, il est également docteur en physique.