Vous êtes ici
Voici le premier modèle physique cohérent sur l’histoire de l’attraction lunaire !

Pour poser le pied sur la Lune en 2027, comme le prévoit la Nasa, les astronautes devront parcourir un trajet plus long que leurs prédécesseurs d’Apollo 11. Environ deux mètres de plus. Tout simplement parce que notre satellite s’éloigne de quelques centimètres tous les ans, et ce en raison de la force de marée qu’exerce la Lune sur la Terre.
Le premier à avoir compris cette mécanique cosmique est George Darwin, le fils du grand Charles. Ce scientifique avait postulé en 1880 que l'attraction de la Lune déformait la Terre en créant un bourrelet qui n'est pas exactement dans la direction de la Lune (voir ci-dessous). L'attraction entre ce bourrelet et notre satellite naturel agit comme un léger frein appliqué sur ces rouages célestes et dissipe un peu de l’énergie du système Terre-Lune. La vitesse de rotation de notre planète devait donc diminuer. Or, en vertu de la conservation de la quantité de mouvement de rotation dans le système Terre-Lune, si la Terre ralentit, la distance entre celle-ci et la Lune doit s’allonger.

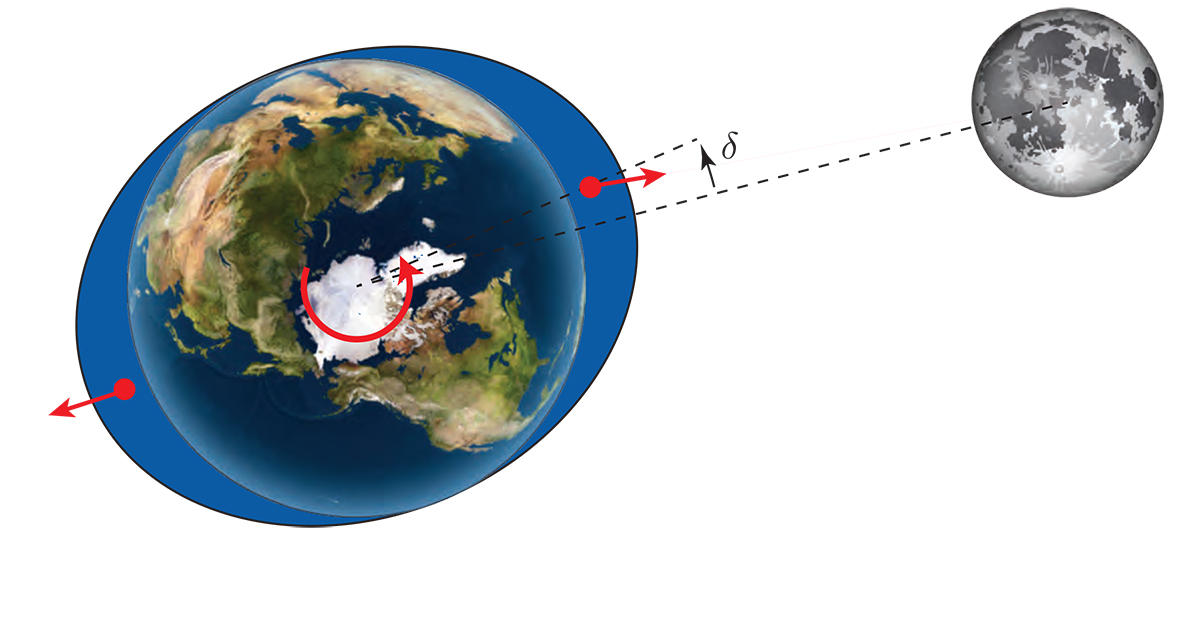
Près d’un siècle plus tard, les horloges atomiques et les mesures laser de la distance entre la Terre et la Lune ont confirmé l’intuition géniale de George Darwin : nos jours s’allongent de deux millisecondes par siècle tandis que la Lune s’écarte du plancher des vaches à la vitesse sidérante de 3,83 centimètres par an.
Un paradoxe vieux de 50 ans
Pourtant, le postulat pose problème. « Si on remonte le temps avec le modèle de George Darwin, on obtient que la Lune se serait formée il y a 1,5 milliard d’années », explique Jacques Laskar, directeur de recherche au CNRS, à l’Institut de mécanique céleste et de calcul des éphémérides1 (IMCCE). « Or, la Lune a 4,4 milliards d’années selon les analyses », en particulier selon les premières datations précises des roches lunaires rapportées par les missions Apollo. D’où un paradoxe qui trouble les scientifiques depuis les années 1970… et qu’une équipe de chercheurs de l'IMCCE vient de résoudre.
« Nous proposons le premier modèle cohérent du système Terre-Lune qui s’ajuste à la fois à l’âge réel de la Lune et à sa vitesse d'éloignement que l’on observe actuellement2 », affirme Jacques Laskar, coordinateur du projet interdisciplinaire AstroGeo3, financé par le Conseil européen de la recherche. Un véritable tour de force qui a demandé aux chercheurs pas moins de dix ans d’efforts et les thèses successives de Pierre Auclair-Desrotour, maintenant astronome-adjoint à l’IMCCE, et de Mohammad Farhat, auteur principal de l’étude.
L’écart entre l’âge réel de la Lune et l’âge calculé avec le modèle de marées de Darwin montrait que celui-ci était incomplet. En effet, dans le modèle du savant anglais, le coefficient qui intervient dans le calcul de la vitesse d'éloignement de la Lune est constant. Dans le modèle actuel, ce n’est plus le cas. Tout se passe alors comme si la « pédale de frein » (due à la force de marée) avait été appuyée puis relâchée alternativement. Ainsi, la décélération de la rotation terrestre a varié significativement au cours du temps. Mais quels paramètres déterminent ces oscillations ? Qu’est ce qui explique ces changements de l’intensité de la force de marée ?
Un modèle physique de la Terre à deux paramètres
Pour définir ces éléments, les chercheurs ont étudié la manière dont l’océan absorbe l’énergie des marées. En effet, c’est essentiellement la friction au fond des océans qui constitue la force de frottement qui ralentit ce jeu de toupies cosmiques. Ils ont donc construit leur modèle physique de façon étonnamment simple : la Terre est divisée en deux éléments hémisphériques, un océan et un supercontinent. Ceux-ci évoluent en fonction de la dérive des continents au cours du dernier milliard d’années pour se fondre en un océan global dans les temps les plus reculés. Seulement deux paramètres suffisent alors à décrire l’évolution de la rotation de la Terre : la dissipation de l’énergie de marée au fond de l’océan et la profondeur de celui-ci.

Une fois le modèle sur pied, il restait une tâche aux chercheurs : le mettre à l’épreuve des données réelles. Il leur fallait montrer que leurs équations décrivaient de façon réaliste l’évolution de la force de marée. Pour cela, ils ont fait appel aux données récoltées par les géologues.
Il se trouve que certains dépôts sédimentaires ont enregistré la fréquence des marées à différents moments de l’histoire de la Terre. D’autres registres géologiques ont inscrit, quant à eux, les changements d’orientation de l’axe de rotation de la Terre, un paramètre qui dépend de l’attraction lunaire. Ainsi, les chercheurs ont pu comparer la courbe produite par leur modèle à ces données stratigraphiques. Résultat : « notre modèle colle très bien aux données géologiques les plus précises », affirme Jacques Laskar. C’était là l’épreuve du feu pour le modèle des chercheurs.
Désormais, grâce à ce résultat, on peut savoir quelle était la vitesse de rotation de la Terre à tout moment depuis qu’elle s’est dotée d’un satellite. Mieux encore : on peut aussi dire comment a varié la distance Terre-Lune au cours des derniers milliards d’années ! « Notre travail permettra d’améliorer les modèles de marée et de mieux comprendre leur évolution au cours de l’histoire terrestre. Il permettra aussi d’affiner les données stratigraphiques décrivant l’orientation de l’axe de la Terre aux temps anciens. » Mais l’impact de ces résultats devrait aller au-delà de la Lune et du Soleil. Après quelques adaptations, ce modèle pourrait en effet être appliqué aux marées océaniques des planètes extrasolaires. ♦
- 1. Unité CNRS/Observatoire de Paris-PSL/Sorbonne Université.
- 2. “The resonant tidal evolution of the Earth-Moon distance”, Astronomy and Astrophysics, sept. 2022. https://www.aanda.org/articles/aa/full_html/2022/09/aa43445-22/aa43445-2...
- 3. Astronomical Solutions over Geological Time.















































