Vous êtes ici
Stéphane Mallat, bâtisseur de ponts mathématiques et informatiques
Temps de lecture : 16 minutes
« On imagine souvent les mathématiques comme un corpus de concepts abstraits, qui s’appliquent “d’en haut” à la réalité, souligne Stéphane Mallat. Mais, la plupart du temps, c’est l’inverse qui se produit : les problèmes du monde nous obligent à construire de nouveaux outils mathématiques. Or, pour les façonner, il faut “mettre les mains dans le cambouis”, construire des ponts entre les abstractions mathématiques et les questions concrètes du monde. Et c’est justement là, sur cette frontière entre les deux, que je me sens bien. »
L’œuvre scientifique du chercheur de 62 ans, grand front surmonté de cheveux ébouriffés, regard doux et bleu et sourire généreux, l’atteste. Ses travaux ont profondément marqué les domaines des mathématiques appliquées au traitement du signal. Il est notamment l’inventeur d’un algorithme clé à l’origine du format JPEG 2000, et du décryptage mathématique des modèles d’apprentissage profond au cœur des intelligences artificielles.



Titulaire de la chaire de science des données au Collège de France et chercheur à l’École normale supérieure, membre de l’Académie des sciences, de la National Academy of Engineering américaine, cosignataire de 10 brevets, lauréat de la médaille de l’innovation du CNRS et de nombreuses autres distinctions internationales, Stéphane Mallat vient donc de se voir décerner la plus prestigieuse de toutes les récompenses scientifiques françaises : la médaille d’Or du CNRS.
« L’extraordinaire puissance et la beauté des concepts abstraits »
Très tôt, le jeune Stéphane se révèle féru de maths – « une bulle dans laquelle je me sentais bien » –, mais elles sont à ses yeux trop éthérées pour qu’il envisage d’en faire son métier. Enfant, il aime « construire des choses, incarner des idées, comme un ingénieur », en faisant de la menuiserie. « Si je suis revenu aux maths, c’est d’ailleurs à la faveur d’intuitions issues d’application. J’ai alors compris l’extraordinaire puissance et la beauté des concepts abstraits, capables de capturer l’essence de réalités en apparence très différentes. »
Après un cursus sans faute à Polytechnique, il s’envole pour l’Université de Pennsylvanie, aux États-Unis, où, en 1988, il soutient une thèse en maths appliquées au traitement d’images sous la direction de Ruzena Bajcsy – « une pionnière du domaine », à une époque où le numérique explose.
Une image de 1000 x 1000 pixels contient 1 million de valeurs numériques. Chaque pixel est un nombre compris entre 0 (noir) et 255 (blanc). Comment extraire de l’information d’une telle avalanche d’octets ? Sa directrice de thèse lui propose d’essayer de le faire en modifiant la résolution des images.
Un nombre minimum de structures élémentaires
Tout au long de sa thèse, puis durant les huit années suivantes, au prestigieux Institut Courant de New York, Stéphane Mallat s’emploie à révéler des principes qui gouvernent l’extraction d’information de toutes sortes de données numériques (des images, des sons, des électrocardiogrammes), avec un objectif en tête : représenter des données de grande taille comme une superposition d’un nombre minimum de structures élémentaires.
« C’est un peu comme si l’on voulait construire une maison en Lego, en utilisant le moins de briques possibles et en se laissant la possibilité de définir la forme de ces briques élémentaires », prend-il soin d’exposer clairement, toujours en souriant et en faisant danser ses mains devant lui à la manière d’un chef d’orchestre.
Cette question de représentation parcimonieuse, qui rappelle le principe de simplicité du rasoir d’Ockham1 en philosophie, se pose dans tous les domaines. En musique par exemple, une mélodie polyphonique est constituée d’une succession de briques élémentaires que sont les notes, chacune dotée d’une hauteur et d’une durée propre.
« Concernant une image, si l’on veut être parcimonieux, il faut se concentrer sur les variations significatives – un contour, un changement abrupt de couleur, détaille Stéphane Mallat. En mathématiques, on tente de capturer l’essence du problème – la recherche de parcimonie – en se libérant du contexte de ces applications spécifiques, pour trouver des solutions générales qui auront ensuite un large champ d’applications. »
Rencontre avec les « ondelettes » d’Yves Meyer
Dès le début de sa carrière, il se met en quête de ces structures essentielles capables de représenter avec parcimonie n’importe quel type de données. La sérendipité va le mettre sur le chemin de ces briques élémentaires.
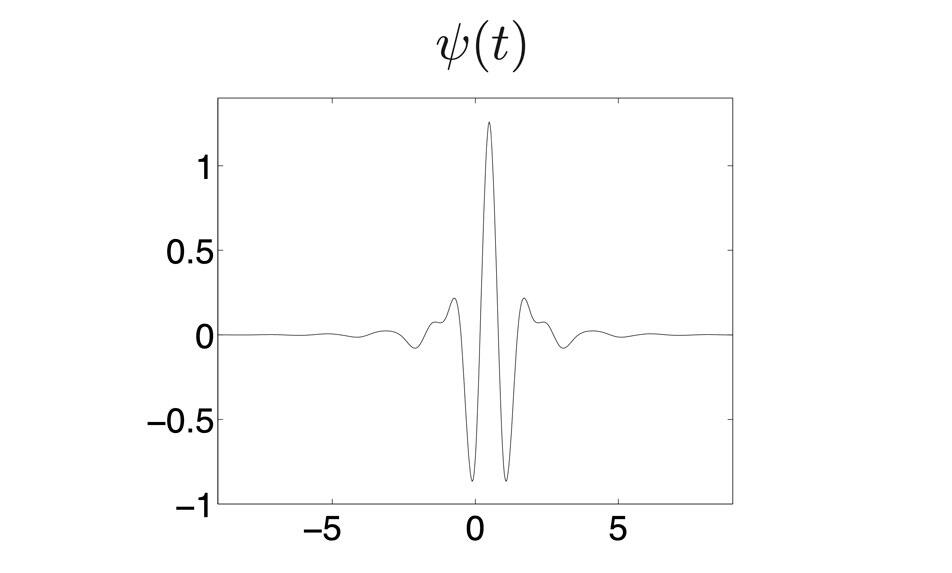
Sur la plage, un été, un ami lui parle des travaux du mathématicien Yves Meyer sur les « ondelettes ». En mathématiques, une ondelette est une courbe qui oscille sur un petit domaine puis s’annule. Intrigué, il se procure son article, qui démontre notamment que l’on peut représenter n’importe quelle courbe complexe comme une superposition d’ondelettes très particulières. Le problème mathématique posé par Yves Meyer était de comprendre s’il était possible de construire d’autres types d’ondelettes pouvant produire des décompositions plus parcimonieuses2.
« J’ai trouvé une solution à cette question mathématique à partir du problème de traitement d’images posé par Ruzena Bajcsy, explique Stéphane Mallat. En traitement d’images, les ondelettes peuvent s’interpréter comme des détails qui augmentent progressivement la résolution des images. En suivant ce chemin, j’ai introduit la théorie des analyses à différentes résolutions, qui permet de construire toutes les ondelettes mathématiques. Ainsi, l’intuition issue du traitement d’images m’a donné la solution du problème mathématique, mais c’est l’abstraction mathématique qui m’a permis de comprendre comment calculer la “transformée en ondelettes”. »
Comprenez : un algorithme rapide qui réécrit n’importe quelle donnée numérique, par exemple une image constituée de millions de pixels, en une superposition d’un nombre beaucoup plus réduit d’ondelettes décrivant chacune une variation locale de l’image.
« Si Ruzena Bajcsy a été mon mentor côté applications, raconte Stéphane Mallat, Yves Meyer a sans conteste été celui de l’abstraction, et je passe toujours de l’un à l’autre. »
Une nouvelle norme mondiale
Puissant, capable de rapidement compresser des images sans perte d’information, l’algorithme de Mallat est au cœur de nombreuses applications émergeant au tournant du millénaire, dont le standard de compression d’images : le JPEG 2000. Sous la houlette du chercheur, le langage mathématique des ondelettes a ainsi engendré une norme mondiale utilisée non seulement dans les logiciels, mais aussi dans de nombreuses bases de données médicales, météorologiques, astronomiques…



Déjà auréolé de succès et reconnu dans le monde entier comme un scientifique avec lequel il faut désormais compter, le bâtisseur de ponts continue sur sa fulgurante lancée. Il entend pousser plus loin encore la sobriété dans la représentation des données dont il est l’artisan : « À l’écrit, avec un vocabulaire réduit, on peut certes dire des choses complexes, mais on s’expose alors au risque de devoir faire de longues périphrases et, in fine, d’être approximatif. Pour produire des phrases plus courtes, plus percutantes, il faut enrichir son vocabulaire. C’est pourquoi j’ai introduit le concept de “dictionnaire mathématique” comprenant un grand nombre de briques élémentaires, plus spécialisées que des ondelettes. »
« D’enseignant-chercheur à CEO »
De retour en France, alors directeur du département de mathématiques de l’École polytechnique depuis 1998, il applique ces résultats en construisant des dictionnaires de bandelettes, pour mieux représenter les images et la géométrie des contours. Ce qui le pousse à changer de vie.
En 2001, avec trois de ses anciens doctorants, il fonde la start-up Let It Wave. « Quasiment du jour au lendemain, je suis passé d’enseignant-chercheur à CEO et j’ai découvert un nouveau monde : le marketing, la négociation des levées de fonds, l’angoisse que l’aventure s’arrête brutalement faute de subsides… C’était passionnant, et par certains aspects, semblable à la recherche : les entrepreneurs ont aussi besoin de s’enthousiasmer comme des gamins pour une idée dont ils pensent qu’elle peut révolutionner le monde, même si elle peut s’effondrer dans les quinze jours. Ils ont une vision, ne sont jamais blasés, ce qui, à mes yeux, est une indispensable qualité. Mais en changeant de monde, j’ai réalisé à quel point la recherche et l’enseignement me manquaient. »
Réseaux de neurones profonds
Trop de concret, pas assez d’abstrait. Alors, après avoir avantageusement vendu Letitwave, il retourne à Polytechnique en 2007, où il crée des cours d’entrepreneuriat pour les étudiants. Une façon de passer le flambeau du bâtisseur.


« Mais, en tant que chercheur, j’ai eu un moment de vide. Je n’avais pas envie de refaire la même chose qu’avant, toutes les idées que j’avais semblaient avoir déjà été explorées… Je doutais, je me disais qu’à 45 ans, j’étais peut-être trop vieux pour reprendre la recherche, inventer de nouvelles maths ou de nouveaux algorithmes… »
Et puis, tout s’est éclairé. En 2008, Stéphane Mallat découvre les résultats de Yann LeCun sur les réseaux de neurones profonds. « Je connaissais suffisamment les applications au traitement d’images pour réaliser que ces programmes informatiques inspirés du cerveau humain n’apportaient pas qu’un simple progrès, mais un véritable changement de paradigme. »
Mystère de l’apprentissage
Stéphane Mallat plonge alors la tête la première dans le monde de l’intelligence artificielle, avec un objectif : élaborer des modèles mathématiques pour comprendre les étonnantes performances des réseaux de neurones.


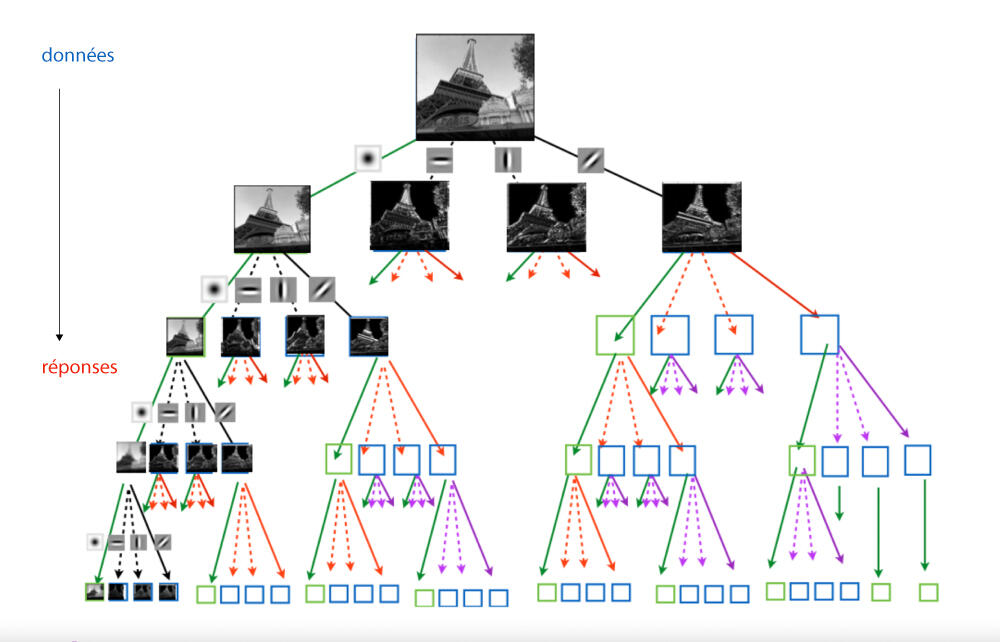
Ces réseaux de neurones apprennent à répondre à une question en analysant une donnée : par exemple, identifier l’animal présent sur une image. Durant leur entraînement, on leur fournit des millions d’exemples avec, à chaque fois, la bonne réponse – le nom de l’animal correspondant à chaque image. Tout comme un élève qui s’entraîne sur des exercices, le réseau apprend en modifiant ses réglages internes pour faire moins d’erreurs.
« Mais comment parvient-il à calculer autant de bonnes réponses sur des nouvelles images qu’il n’a jamais vues ? C’est un mystère, car ces problèmes sont très complexes, insiste le chercheur. Quel type d’informations a-t-il appris à extraire des données ? J’observais que ces réseaux de neurones calculent au départ une “transformée en ondelettes”. Cela me rappelait les résultats de neurophysiologistes, qui ont aussi trouvé des “transformées en ondelettes” dans les premières aires de notre cortex visuel, ainsi que dans la cochlée de l’oreille. »
Les bases mathématiques des modèles d’apprentissage profonds
Fort de son expertise et de cette vision interdisciplinaire, Stéphane Mallat montre qu’un réseau de neurones construit des représentations hiérarchiques. Il sépare les plus grandes structures (par exemple, le contour grossier d’un visage dans une image) et représente les composantes plus fines relativement aux composantes plus larges (par exemple, les yeux relativement au visage, puis la pupille relativement à l’œil).
« La transformée en ondelettes est une première étape pour construire cette hiérarchie », précise Mallat.
En levant ce mystère, le chercheur a jeté des bases mathématiques des modèles d’apprentissage profonds, sur lesquelles reposent aujourd’hui bon nombre d’IA modernes. « Mais plus on avance dans les couches des réseaux, plus ces derniers détectent des structures sophistiquées, précise-t-il. Certains neurones s’activent pour des choses très précises, comme une mélodie ou un visage. C’est comme si ces couches profondes représentaient les données avec des “dictionnaires mathématiques” très riches et très spécialisés, mais dont les propriétés restent mal comprises par les scientifiques. »
Contrôler et réguler les intelligences artificielles
Tous ces résultats, insiste-t-il, ont été obtenus collectivement : « En science, on n’avance quasiment jamais seul. Tout au long de ma carrière, j’ai beaucoup travaillé avec mes doctorantes et doctorants, et de nombreux collaborateurs et collaboratrices. Ils et elles m’ont accompagné pour formuler les bonnes questions, partager les succès aussi bien que les coups durs. Chacun à sa manière, a apporté des contributions fondamentales. »
Menacent-elles nos sociétés, ces intelligences artificielles sur lesquelles Stéphane Mallat planche encore aujourd’hui ? « Elles sont porteuses de fabuleux progrès, par exemple en médecine, mais, comme toute technologie, elles présentent aussi des dangers – pour le respect de la vie privée et à cause de leur potentielle utilisation militaire… Il est donc indispensable de les contrôler et de réguler, estime le chercheur, mais ce n’est pas qu’une affaire de gouvernements. »
« J’adore danser »
« Chacun d’entre nous est confronté à cette révolution, poursuit le chercheur, et aura besoin de s’adapter pour profiter du meilleur tout en évitant les dérives. Cela nécessite de comprendre l’IA, de ne pas la mythifier. C’est notamment dans ce but que j’ai créé MathAData3, un programme d’enseignement des mathématiques au lycée, en lien direct avec la résolution de problèmes pratiques d’IA. On voit que collégiens et lycéens sont bien plus motivés à apprendre les maths si on leur montre qu’elles sont au centre de grandes questions et d’outils de leur quotidien. »
Que faites-vous, Stéphane Mallat, quand vous ne naviguez pas dans un océan de données, quand vous ne bâtissez pas des ponts entre les grandes idées et la réalité ? « J’adore danser. Le tango, le rock… parfois sur les quais de Seine. Quand je danse, je suis dans un autre monde, celui de la musique et de ma partenaire. Je déconnecte. » Tous les bâtisseurs n’ont-ils pas besoin de parfois souffler ? ♦
Consultez aussi
Reportage photo dans le laboratoire de Stéphane Mallat à l’ENS
Indispensables mathématiques (dossier)
- 1. Rasoir d’Ockham : inspiré des écrits du philosophe Guillaume d’Ockham (XIVe siècle ), ce principe stipule que si plusieurs hypothèses peuvent expliquer un phénomène, l’hypothèse la plus simple est la plus vraisemblable.
- 2. Ou, dit en langage mathématique : « construire des nouvelles bases orthogonales avec des ondelettes ».
- 3. Enseigner les Mathématiques du Lycée par des challenges d'IA : https://mathadata.fr/fr
Voir aussi
Auteur
Journaliste scientifique avec une appétence particulière pour l’astronomie et les reportages de terrain, Émilie Martin est cheffe de rubrique au magazine Ciel & Espace, auteure de documentaires pour la télévision et collabore régulièrement à des projets de muséographie scientifique.